문제 링크
풀이
이항 계수의 식과, 페르마의 소정리, 모듈러 연산을 알아야 풀 수 있는 문제
보통 이항 계수 문제는 DP나 재귀로 풀 수 있는데 입력값이 너무 크기 때문에 시간 초과가 난다.
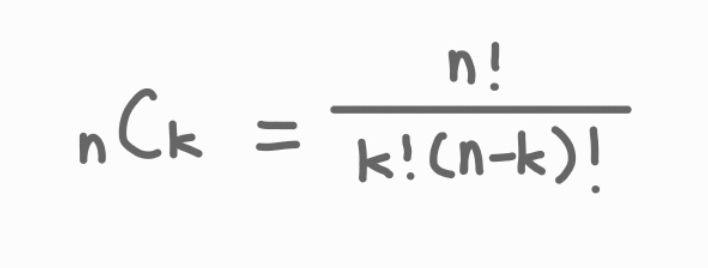
이런 경우 공식을 이용해 풀어야한다.

우리가 구해야 할 것은 이항 계수를 1000000007 (이하 mod)로 나눈 값이다.
해당 값을 바로 구할 수 있다면 좋겠지만 분수의 나머지 구하기는 힘들기 때문에 페르마의 소정리를 이용해야 한다.
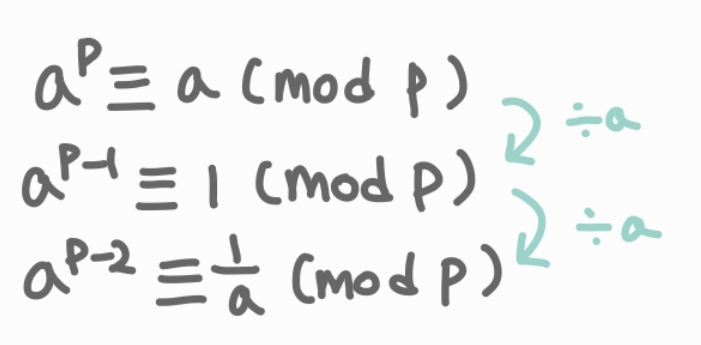
페르마의 소정리란 p가 소수일 때,
a^p를 p로 나눈 나머지가 a를 p로 나눈 나머지와 같다는 정리이다.
해당 식을 변형해서 맨 마지막 식까지 만들 수 있고 저 식을 우리가 구해야 하는 값의 공식에 적용할 것이다.
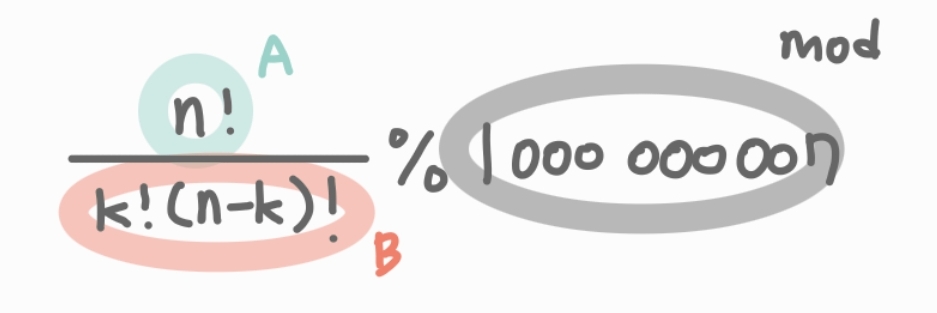
이항계수의 분자를 A, 분모를 B, 나머지를 mod라고 한다면,
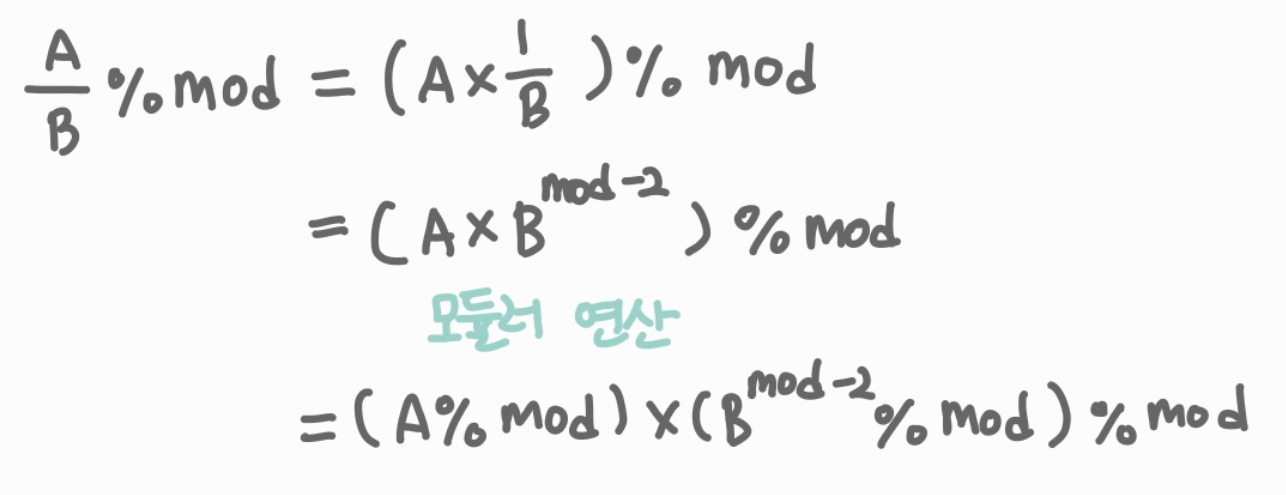
해당 식이 만들어질 것이다.
중간의 모듈러 연산은 (a*b)%mod = (a%mod)*(b%mod)%mod 이다.
이제 식이 다 만들어졌으니 코드만 작성하면 된다.
B^(mod-2) 구하는 과정에서 분할 정복을 사용해서 이 문제가 분할 정복 분류로 들어간 것 같다.
거듭제곱의 공식은 간단하게 2^5 = 2 * 2^2 * 2^2 와 같이 거듭제곱 값을 반으로 쪼개서 구하면 된다.
여기서도 마찬가지로 모듈러 연산을 사용하면 된다.
해당 알고리즘의 시간복잡도는 팩토리얼 구하기 O(n) + 거듭제곱 구하기 O(log n)이 되어 O(n)의 시간복잡도로 풀 수 있는 것 같다.
이 문제를 나중에도 풀 수 있을지는 의문이다... 알고리즘 자체가 엄청 어렵지는 않은데 공식을 까먹으면 못 푸는 문제네
코드
#include <iostream>
using namespace std;
long long mod = 1000000007;
long long power(long long a, long long b)
{
if (b == 0) return 1;
if (b % 2 == 1) return (power(a, b - 1)*a) % mod;
long long half = power(a, b / 2) % mod;
return (half*half) % mod;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, k;
cin >> n >> k;
long long a = 1; // n!
long long b = 1; // k!(n-k)!
for (int i = 1; i <= n; i++)
{
a *= i;
a %= mod;
}
for (int i = 1; i <= n - k; i++)
{
b *= i;
b %= mod;
}
for (int i = 1; i <= k; i++)
{
b *= i;
b %= mod;
}
long long answer = (a%mod)*(power(b, mod - 2) % mod) % mod;
cout << answer << endl;
return 0;
}