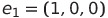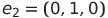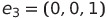'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[3장]
데카르트 좌표계
데카르트 좌표계 : 직선의 수 집합을 수직으로 배치해 평면을 표기하는 방식
좌표 : 데카르트 좌표계의 한 원소는 곱집합과 동일하게 순서쌍으로 표현
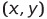
좌표는 점 또는 원점으로부터의 화살표로 표현, 크기와 방향 두가지 속성을 지님
벡터 공간과 벡터
스칼라와 벡터
벡터의 표기
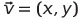
벡터 공간의 연산
- 벡터와 벡터의 덧셈(벡터의 합)
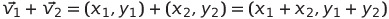
- 스칼라와 벡터의 곱셈(스칼라 곱셈)
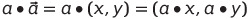
벡터 공간의 공리
- 벡터의 합의 결합법칙
- 벡터의 합의 교환법칙
- 벡터의 합의 항등원
- 벡터의 합의 역원
- 스칼라 곱셈의 호환성
- 스칼라 곱셈의 항등원
- 벡터의 합에 대한 분배법칙
- 스칼라 덧셈에 대한 분배법칙
벡터의 크기와 이동
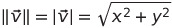
단위 벡터 : 크기가 1인 벡터
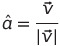
벡터의 결합과 생성
선형 결합 : n개의 스칼라와 n개의 벡터를 결합해 새로운 벡터를 생성하는 수식
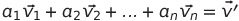
새로운 벡터를 영벡터가 나오게 하는 수식을 생각했을 때,
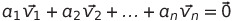
모든 스칼라 값이 0이면 선형 결합의 결과는 영벡터가 됨
그렇지만 a가 0이 아닌 경우에도 영벡터는 나올 수 있음 → 선형 종속의 관계
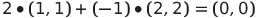
영벡터가 나오기 위해 모든 a값이 0이어야 한다면 → 선형 독립의 관계
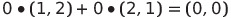
선형 독립 관계(기저, Basis) : 평면의 모든 벡터를 만들 수 있음,
두 벡터가 평행하면 안되고, 2개의 벡터의 결합만 가능
기저의 개념은 차원이라는 새로운 용어를 정의하는데 사용
기저 집합의 원소 수는 언제나 2개뿐, 평면에 대응하는 벡터 공간을 2차원으로 정의 가능
→ 2차원 실벡터 공간(ℝ²)
표준 기저 : 단위 벡터 (1,0), (0,1)로 구성된 집합
각 원소를 표준기저벡터
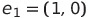
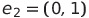
벡터 공간의 차원에는 제약이 없음
ℝ³
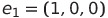
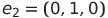
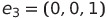
'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[3장]
데카르트 좌표계
데카르트 좌표계 : 직선의 수 집합을 수직으로 배치해 평면을 표기하는 방식
좌표 : 데카르트 좌표계의 한 원소는 곱집합과 동일하게 순서쌍으로 표현
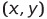
좌표는 점 또는 원점으로부터의 화살표로 표현, 크기와 방향 두가지 속성을 지님
벡터 공간과 벡터
스칼라와 벡터
벡터의 표기
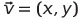
벡터 공간의 연산
- 벡터와 벡터의 덧셈(벡터의 합)
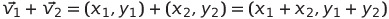
- 스칼라와 벡터의 곱셈(스칼라 곱셈)
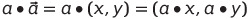
벡터 공간의 공리
- 벡터의 합의 결합법칙
- 벡터의 합의 교환법칙
- 벡터의 합의 항등원
- 벡터의 합의 역원
- 스칼라 곱셈의 호환성
- 스칼라 곱셈의 항등원
- 벡터의 합에 대한 분배법칙
- 스칼라 덧셈에 대한 분배법칙
벡터의 크기와 이동
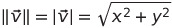
단위 벡터 : 크기가 1인 벡터
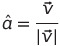
벡터의 결합과 생성
선형 결합 : n개의 스칼라와 n개의 벡터를 결합해 새로운 벡터를 생성하는 수식
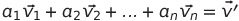
새로운 벡터를 영벡터가 나오게 하는 수식을 생각했을 때,
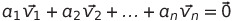
모든 스칼라 값이 0이면 선형 결합의 결과는 영벡터가 됨
그렇지만 a가 0이 아닌 경우에도 영벡터는 나올 수 있음 → 선형 종속의 관계
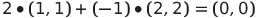
영벡터가 나오기 위해 모든 a값이 0이어야 한다면 → 선형 독립의 관계
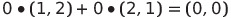
선형 독립 관계(기저, Basis) : 평면의 모든 벡터를 만들 수 있음,
두 벡터가 평행하면 안되고, 2개의 벡터의 결합만 가능
기저의 개념은 차원이라는 새로운 용어를 정의하는데 사용
기저 집합의 원소 수는 언제나 2개뿐, 평면에 대응하는 벡터 공간을 2차원으로 정의 가능
→ 2차원 실벡터 공간(ℝ²)
표준 기저 : 단위 벡터 (1,0), (0,1)로 구성된 집합
각 원소를 표준기저벡터
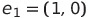
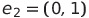
벡터 공간의 차원에는 제약이 없음
ℝ³