'이득우의 게임 수학' 책을 보고 정리한 포스팅입니다.
[6장]
이동 변환을 위한 아핀 공간
2 × 2 정방 행렬의 곱셈으로 2차원 평면에서의 이동 구현 X
임의의 벡터 (x,y)를 (a,b)만큼 이동시키는 기능 → 행렬의 덧셈으로
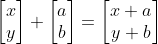
하지만 행렬 곱을 만족하는 정방행렬 A는 존재 X
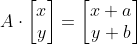
표준기저벡터의 원점 이동 변환이 행렬이 되기 위해서는 선형성을 만족해야하는데,
선형성이 되기 위해서 기저벡터는 원점에서부터 출발해야 함
차원을 늘리면 구현이 가능
→ 두 개의 차원은 물체 표현, 한 개의 차원은 선형 변환을 위한 원점과의 연결고리
전단 변환의 성질을 통해 y값을 1로 적용하면 선형 변환시 다음과 같은 수식이 성립
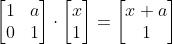
→ 이를 통해 1차원의 이동 변환을 할 수 있음
→ 마찬가지로 2차원의 이동 변환을 위해서는? 3차원을 사용
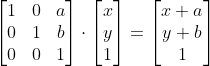
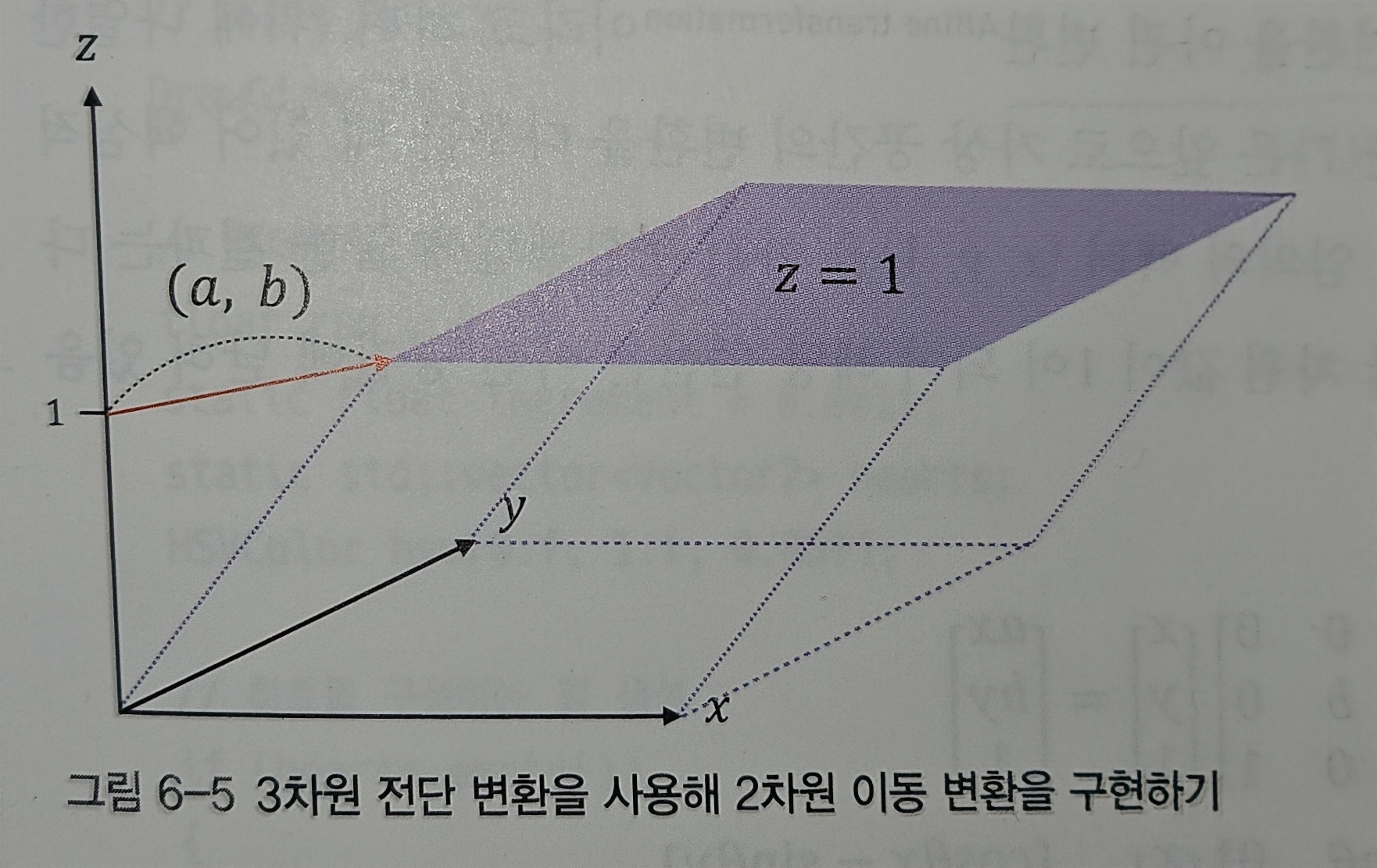
이동 변환행렬
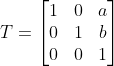
이동에 사용되는 벡터의 마지막 차원 값은 1
이동에 사용되는 벡터를 (x,y,1)로 지정
벡터 공간에서 이동을 위해 마지막 차원 값을 1로 한정한 부분 공간
⇒ 아핀 공간 (Affine Space)
크기, 회전 변환행렬은 2×2 정방행렬이고, 이동 변환 행렬은 3×3 정방 행렬이라
행렬 곱의 장점(결합법칙)을 위해 S,R,T 세 행렬의 크기를 같게 해야함
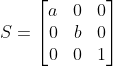
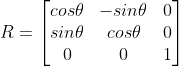
⇒ 아핀 변환 : 한 차원 높여 설계한 선형 변환
임의의 벡터 (x,y,1)을 아핀 변환행렬에 곱한 결과는 모두 마지막 차원 값이 1
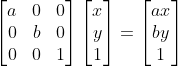
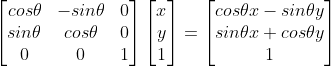
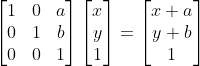
아핀 공간의 구성 요소
점
점 : 마지막 차원 값이 1인 아핀 공간의 원소
점의 성질 :행렬 곱을 사용해 이동이 가능
가상 공간이 이동하려면 물체는 점으로 구성되어야 함
2차원 공간의 점 : (x,y,1)
3차원 공간의 점 : (x,y,z,1)
이동 벡터
벡터는 아핀 공간 내의 이동을 지정하기 위해 사용
아핀 공간의 벡터 : 이동 벡터, 변위 벡터
아핀 공간의 점 P1에 이동 벡터 v를 더하면 다른 점 P2에 대응
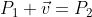
이동 벡터
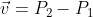
P1의 좌표 (x1, y1, 1), P2의 좌표 (x2, y2, 1)을 빼면
이동 벡터의 형태
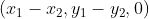
마지막 차원인 z값이 항상 0인 영역 형성
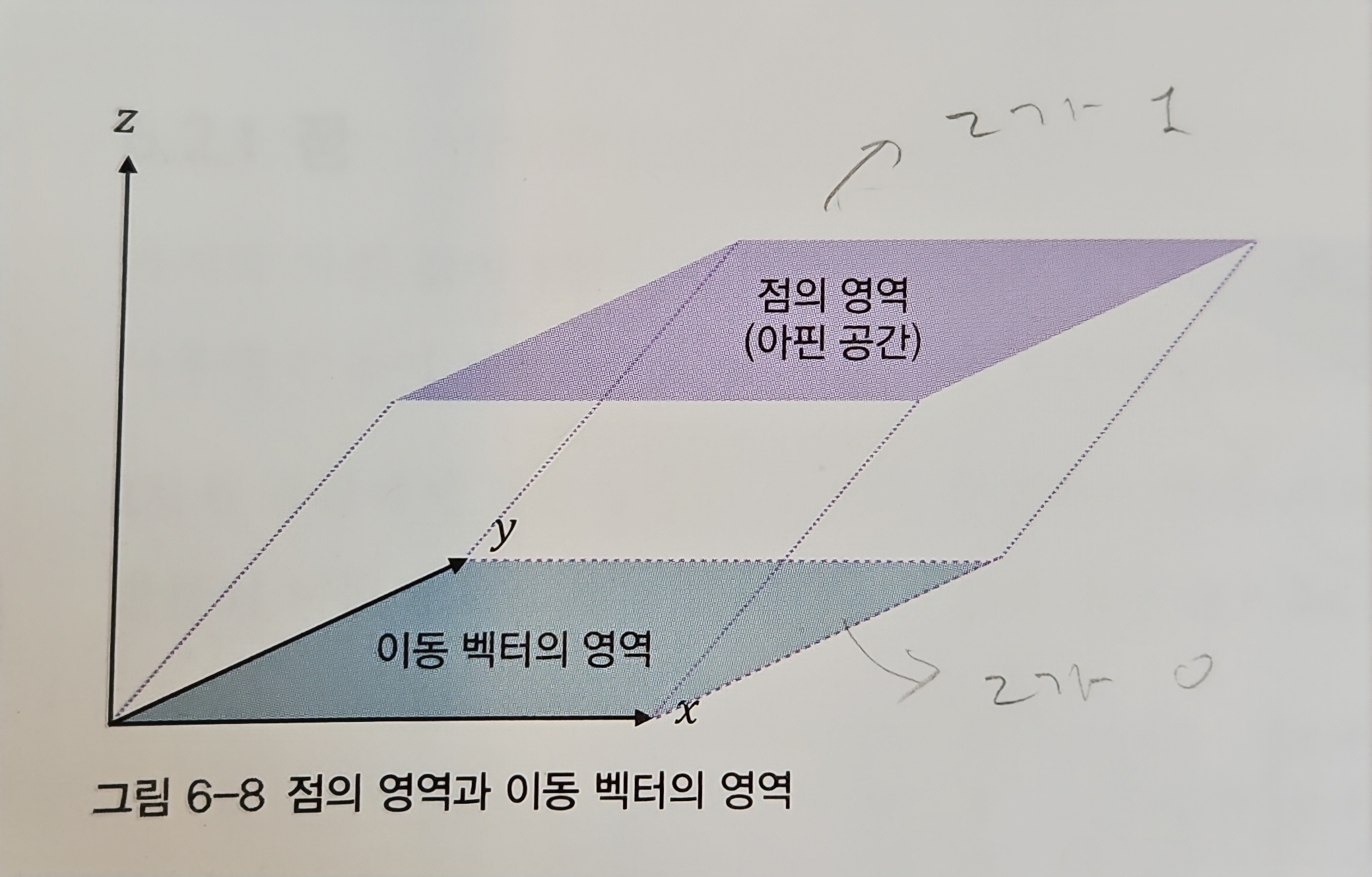
아핀 공간의 성질
아핀 공간의 중심인 원점 O의 값 (0,0,1)
아핀 공간에 속한 임의의 점 P의 값 (x,y,1)
원점 O에서 점 P로 향하는 이동벡터 v
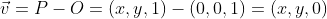
→ 점과 벡터 덧셈 연산은 아핀 공간에 대해 닫혀 있음
유클리드 공간 : 현실 세계의 3차원 공간, 아핀 공간에 대응
유클리드 공간에서 작용되는 힘 : 유클리드 벡터, 이동 벡터에 대응
점 : 물체를 표현, 위치 지정에 사용. 마지막 차원 값은 1
이동 벡터 : 물체를 움직이는 데 사용. 마지막 차원 값은 0
- 점 - 점 : 벡터
- 점 + 벡터 : 점
- 벡터 + 벡터 = 벡터
- 점 + 점 ≠ 점
아핀 결합
점과 점을 더한 결과는 사용할 수 없지만,
점과 점을 더할 때 선형 결합의 형태로 점에 스칼라를 곱해 더한다면, 특정 조건에서 새로운 점 생성 가능
P1(x1,y1,1) P2(x2,y2,1)에 각각 스칼라 a,b를 곱한 선형 결합의 식
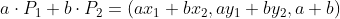
두 점의 선형 결합 결과가 점이 되려면 마지막 차원 값 a+b가 1이 되어야 함
→ 모든 스칼라의 합이 1이 되면 됨
아핀 결합 : 여러 개의 점을 결합해 새로운 점 생성하는 수식
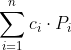
두 점의 결합
a+b=1 을 통해 b를 1-a로 바꿈
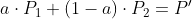
a에 각각 1과 0을 대입하면 다음과 같음
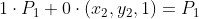
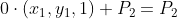
→ 점 P1, P2의 아핀 결합으로 새로운 점을 생성하면,
a값이 양의 방향으로 커질수록 P1의 바깥쪽 방향에 점이 생김
a값이 음의 방향으로 커질수록 P2의 바깥쪽 방향에 점이 생김
P1과 P2를 지나는 무한한 긴 선
직선의 방정식
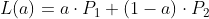
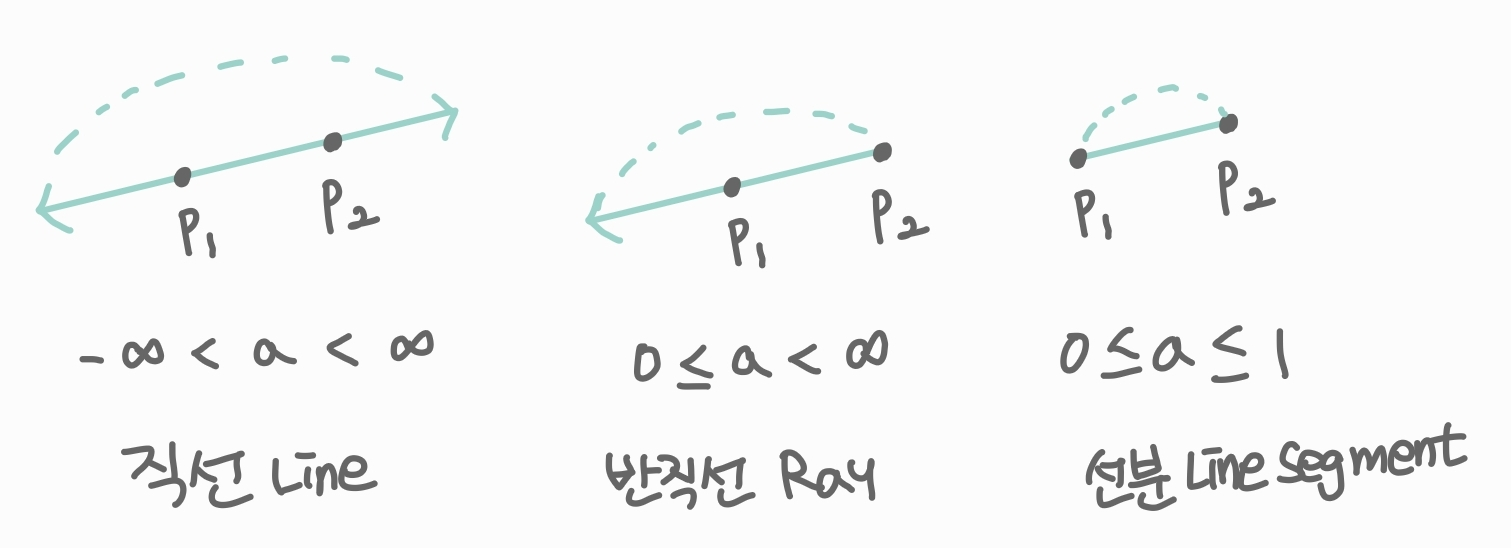
직선의 방정식의 a의 범위에 따라 다양한 종류의 선 대응
직선(Line) : 두 점의 양쪽 방향으로 무한히 뻗어나가는 선
반직선(Ray) : 지정한 위치에서 한쪽 방향으로만 뻗어나가는 선
ex) 레이캐스팅, 레이트레이싱 ..
선분(Line Segment) : 시작점과 끝점의 위치가 정해진 선
선 그리기 알고리즘
벡터를 모니터의 점으로 표현
모니터 화면의 좌표계는 y축이 아래쪽을 향함
→ 스크린 좌표계
스크린 좌표계의 특징 : 실수가 아닌 정수 사용 → 하나의 스크린 좌표는 네모난 영역에 대응
픽셀(Pixel) : 스크린 좌표와 색상에 대응하는 화면의 구성 요소
픽셀화(Rasterization) : 실수로 표현된 벡터 좌표를 정수로 변환 후 색상 부여하는 과정
픽셀화 과정 주요 사항 : 화면 해상도가 짝수인 경우, 데카르트 좌표계의 원점인 (0,0)을 픽셀로 표현하기 위해 중앙을 공유하는 네 픽셀 중 하나를 선택
스크린 좌표를 벡터로 변환해야하는 경우도 규칙을 정해야 함
데카르트 좌표계와 스크린 좌표계의 차이
| 데카르트 좌표계 | 스크린 좌표계 | |
| 수 집합 | 실수 | 정수 |
| 수의 성질 | 연속성 | 이산성 |
| 단위 원소 | 벡터 | 픽셀 |
| 수의 범위 | 실수 범위 | 0부터 해상도 크기까지 |
선 그리기 알고리즘
직선의 방정식이 아닌, 선을 구성하는 데 필요한 픽셀만 얻어내는 방법
브레젠험 알고리즘
- 화면을 8등분 영역으로 구분 후 영역별로 그려내는 방식
- y축이 아래로 증가하는 스크린 좌표계에서 구현
- 시계 방향
1팔분면
[0º, 45º] 범위 → 기울기 1을 넘어설 수 없음
⇒ 평행하거나 한 칸만 아래로 내려가는 특징
- 시작 위치의 픽셀 (x₀,y₀)을 찍는다.
- 오른쪽 위치의 픽셀을 어디에 찍을지 고려한다.
- 평행하게 찍거나 (x₀+1, y₀), 오른쪽 아래에 찍거나 (x₀+1, y₀+1)의 중점 좌표와 직선의 방정식(판별식)을 비교해 판별식이 0보다 작다면 수평으로 찍고, 크면 아래에 찍는다.
- 평행하게 이동하면 x값만 증가하고 판별식에 2h를 더한다.
- 아래로 이동하면 x와 y값이 증가하고 판별식에 2h-2w를 더한다.
- 마지막 점까지 도달했다면 종료
2팔분면
기울기가 1을 넘음
1팔분면의 x와 y가 바뀜
판별식도 w와 h가 바뀜
라인 클리핑 알고리즘
클리핑 : 선분이 가진 성질은 유지하면서 지정된 영역에 맞는 데이터로 재설정하는 작업
→ 화면 밖에 안보이는 부분은 잘라주는 과정
코헨-서덜랜드 라인 클리핑 알고리즘
9개의 영역으로 설정 : 화면과 그 바깥 영역
| 1001 | 1000 | 1010 |
| 0001 | 0000 | 0010 |
| 0101 | 0100 | 0110 |
상위 두비트는 상하 정보, 하위 두 비트는 좌우 정보
가운데 0000의 영역은 화면의 영역
시작점과 끝점이 0000에 있다면 상관 없지만 하나라도 바깥 영역에 있다면 클리핑 해야 함
→ 그리지 않아도 되는 상황이 생길 수 있음
다음과 같은 세 가지 상황으로 나눠짐
- 화면 안에 위치해서 자를 필요 X
- 화면 밖에 위치해 있어 그릴 필요 X
- 화면을 가로질러서 화면에 유효한 영역으로 잘라내야 하는 경우
시작점과 끝점 두개의 영역 값을 & 연산을 통해 파악 가능
- 두 점이 동일한 가로나 세로에 위치할 경우 & 연산을 하면 0보다 큰 값이 나옴 → 선 그리기 필요 없음
- 두 점이 대각선 반대 방향에 위치할 경우 & 연산을 하면 0 값이 나옴 → 클리핑 필요
- 근데 0001, 1000과 같이 대각선에 있어도 0값이 나오는 경우가 있음 → 한 점을 클리핑하고, 다시 테스트하면 0보다 큰 값이 나와 건너뛰게 됨
'이득우의 게임 수학' 책을 보고 정리한 포스팅입니다.
[6장]
이동 변환을 위한 아핀 공간
2 × 2 정방 행렬의 곱셈으로 2차원 평면에서의 이동 구현 X
임의의 벡터 (x,y)를 (a,b)만큼 이동시키는 기능 → 행렬의 덧셈으로
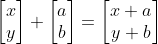
하지만 행렬 곱을 만족하는 정방행렬 A는 존재 X
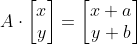
표준기저벡터의 원점 이동 변환이 행렬이 되기 위해서는 선형성을 만족해야하는데,
선형성이 되기 위해서 기저벡터는 원점에서부터 출발해야 함
차원을 늘리면 구현이 가능
→ 두 개의 차원은 물체 표현, 한 개의 차원은 선형 변환을 위한 원점과의 연결고리
전단 변환의 성질을 통해 y값을 1로 적용하면 선형 변환시 다음과 같은 수식이 성립
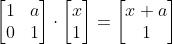
→ 이를 통해 1차원의 이동 변환을 할 수 있음
→ 마찬가지로 2차원의 이동 변환을 위해서는? 3차원을 사용
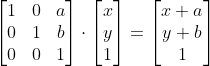

이동 변환행렬
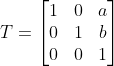
이동에 사용되는 벡터의 마지막 차원 값은 1
이동에 사용되는 벡터를 (x,y,1)로 지정
벡터 공간에서 이동을 위해 마지막 차원 값을 1로 한정한 부분 공간
⇒ 아핀 공간 (Affine Space)
크기, 회전 변환행렬은 2×2 정방행렬이고, 이동 변환 행렬은 3×3 정방 행렬이라
행렬 곱의 장점(결합법칙)을 위해 S,R,T 세 행렬의 크기를 같게 해야함
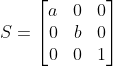
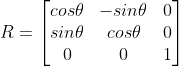
⇒ 아핀 변환 : 한 차원 높여 설계한 선형 변환
임의의 벡터 (x,y,1)을 아핀 변환행렬에 곱한 결과는 모두 마지막 차원 값이 1
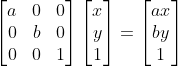
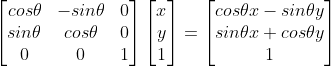
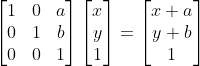
아핀 공간의 구성 요소
점
점 : 마지막 차원 값이 1인 아핀 공간의 원소
점의 성질 :행렬 곱을 사용해 이동이 가능
가상 공간이 이동하려면 물체는 점으로 구성되어야 함
2차원 공간의 점 : (x,y,1)
3차원 공간의 점 : (x,y,z,1)
이동 벡터
벡터는 아핀 공간 내의 이동을 지정하기 위해 사용
아핀 공간의 벡터 : 이동 벡터, 변위 벡터
아핀 공간의 점 P1에 이동 벡터 v를 더하면 다른 점 P2에 대응
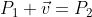
이동 벡터
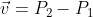
P1의 좌표 (x1, y1, 1), P2의 좌표 (x2, y2, 1)을 빼면
이동 벡터의 형태
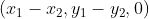
마지막 차원인 z값이 항상 0인 영역 형성

아핀 공간의 성질
아핀 공간의 중심인 원점 O의 값 (0,0,1)
아핀 공간에 속한 임의의 점 P의 값 (x,y,1)
원점 O에서 점 P로 향하는 이동벡터 v
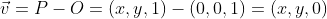
→ 점과 벡터 덧셈 연산은 아핀 공간에 대해 닫혀 있음
유클리드 공간 : 현실 세계의 3차원 공간, 아핀 공간에 대응
유클리드 공간에서 작용되는 힘 : 유클리드 벡터, 이동 벡터에 대응
점 : 물체를 표현, 위치 지정에 사용. 마지막 차원 값은 1
이동 벡터 : 물체를 움직이는 데 사용. 마지막 차원 값은 0
- 점 - 점 : 벡터
- 점 + 벡터 : 점
- 벡터 + 벡터 = 벡터
- 점 + 점 ≠ 점
아핀 결합
점과 점을 더한 결과는 사용할 수 없지만,
점과 점을 더할 때 선형 결합의 형태로 점에 스칼라를 곱해 더한다면, 특정 조건에서 새로운 점 생성 가능
P1(x1,y1,1) P2(x2,y2,1)에 각각 스칼라 a,b를 곱한 선형 결합의 식
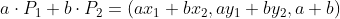
두 점의 선형 결합 결과가 점이 되려면 마지막 차원 값 a+b가 1이 되어야 함
→ 모든 스칼라의 합이 1이 되면 됨
아핀 결합 : 여러 개의 점을 결합해 새로운 점 생성하는 수식
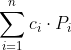
두 점의 결합
a+b=1 을 통해 b를 1-a로 바꿈
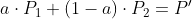
a에 각각 1과 0을 대입하면 다음과 같음
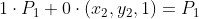
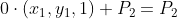
→ 점 P1, P2의 아핀 결합으로 새로운 점을 생성하면,
a값이 양의 방향으로 커질수록 P1의 바깥쪽 방향에 점이 생김
a값이 음의 방향으로 커질수록 P2의 바깥쪽 방향에 점이 생김
P1과 P2를 지나는 무한한 긴 선
직선의 방정식
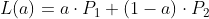
직선의 방정식의 a의 범위에 따라 다양한 종류의 선 대응
직선(Line) : 두 점의 양쪽 방향으로 무한히 뻗어나가는 선
반직선(Ray) : 지정한 위치에서 한쪽 방향으로만 뻗어나가는 선
ex) 레이캐스팅, 레이트레이싱 ..
선분(Line Segment) : 시작점과 끝점의 위치가 정해진 선

선 그리기 알고리즘
벡터를 모니터의 점으로 표현
모니터 화면의 좌표계는 y축이 아래쪽을 향함
→ 스크린 좌표계
스크린 좌표계의 특징 : 실수가 아닌 정수 사용 → 하나의 스크린 좌표는 네모난 영역에 대응
픽셀(Pixel) : 스크린 좌표와 색상에 대응하는 화면의 구성 요소
픽셀화(Rasterization) : 실수로 표현된 벡터 좌표를 정수로 변환 후 색상 부여하는 과정
픽셀화 과정 주요 사항 : 화면 해상도가 짝수인 경우, 데카르트 좌표계의 원점인 (0,0)을 픽셀로 표현하기 위해 중앙을 공유하는 네 픽셀 중 하나를 선택
스크린 좌표를 벡터로 변환해야하는 경우도 규칙을 정해야 함
데카르트 좌표계와 스크린 좌표계의 차이
| 데카르트 좌표계 | 스크린 좌표계 | |
| 수 집합 | 실수 | 정수 |
| 수의 성질 | 연속성 | 이산성 |
| 단위 원소 | 벡터 | 픽셀 |
| 수의 범위 | 실수 범위 | 0부터 해상도 크기까지 |
선 그리기 알고리즘
직선의 방정식이 아닌, 선을 구성하는 데 필요한 픽셀만 얻어내는 방법
브레젠험 알고리즘
- 화면을 8등분 영역으로 구분 후 영역별로 그려내는 방식
- y축이 아래로 증가하는 스크린 좌표계에서 구현
- 시계 방향
1팔분면
[0º, 45º] 범위 → 기울기 1을 넘어설 수 없음
⇒ 평행하거나 한 칸만 아래로 내려가는 특징
- 시작 위치의 픽셀 (x₀,y₀)을 찍는다.
- 오른쪽 위치의 픽셀을 어디에 찍을지 고려한다.
- 평행하게 찍거나 (x₀+1, y₀), 오른쪽 아래에 찍거나 (x₀+1, y₀+1)의 중점 좌표와 직선의 방정식(판별식)을 비교해 판별식이 0보다 작다면 수평으로 찍고, 크면 아래에 찍는다.
- 평행하게 이동하면 x값만 증가하고 판별식에 2h를 더한다.
- 아래로 이동하면 x와 y값이 증가하고 판별식에 2h-2w를 더한다.
- 마지막 점까지 도달했다면 종료
2팔분면
기울기가 1을 넘음
1팔분면의 x와 y가 바뀜
판별식도 w와 h가 바뀜
라인 클리핑 알고리즘
클리핑 : 선분이 가진 성질은 유지하면서 지정된 영역에 맞는 데이터로 재설정하는 작업
→ 화면 밖에 안보이는 부분은 잘라주는 과정
코헨-서덜랜드 라인 클리핑 알고리즘
9개의 영역으로 설정 : 화면과 그 바깥 영역
| 1001 | 1000 | 1010 |
| 0001 | 0000 | 0010 |
| 0101 | 0100 | 0110 |
상위 두비트는 상하 정보, 하위 두 비트는 좌우 정보
가운데 0000의 영역은 화면의 영역
시작점과 끝점이 0000에 있다면 상관 없지만 하나라도 바깥 영역에 있다면 클리핑 해야 함
→ 그리지 않아도 되는 상황이 생길 수 있음
다음과 같은 세 가지 상황으로 나눠짐
- 화면 안에 위치해서 자를 필요 X
- 화면 밖에 위치해 있어 그릴 필요 X
- 화면을 가로질러서 화면에 유효한 영역으로 잘라내야 하는 경우
시작점과 끝점 두개의 영역 값을 & 연산을 통해 파악 가능
- 두 점이 동일한 가로나 세로에 위치할 경우 & 연산을 하면 0보다 큰 값이 나옴 → 선 그리기 필요 없음
- 두 점이 대각선 반대 방향에 위치할 경우 & 연산을 하면 0 값이 나옴 → 클리핑 필요
- 근데 0001, 1000과 같이 대각선에 있어도 0값이 나오는 경우가 있음 → 한 점을 클리핑하고, 다시 테스트하면 0보다 큰 값이 나와 건너뛰게 됨
