[KUOCW] 한정현 컴퓨터그래픽스를 듣고 정리한 포스팅입니다.
행렬과 벡터 (Matrices and Vector)
행렬의 곱
m×n 행렬이 있을 때, m=n이라면 정사각 행렬
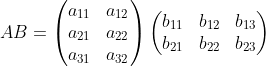
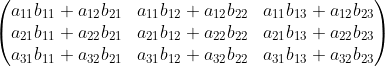
A 행렬 l×m과 B 행렬 m×n은 A의 열 개수와 B의 행 개수가 같아 곱할 수 있음 => l×n 행렬
2D 벡터 (x,y), 3D 벡터 (x,y,z) => row vector (행 벡터)
column vector (열 벡터)로도 표현 가능
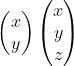
열벡터 (Column Vector)와 행벡터 (Row Vector), 전치 행렬 (Transpose)
벡터를 행렬로 바꾸어 연산을 한다면 다음과 같음
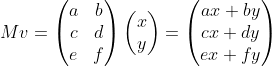
전치 행렬(Transpose)은 다음과 같음
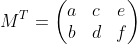
그래서 벡터의 전치 행렬과, 행렬의 전치 행렬을 곱한 값은 다음과 같다.

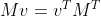
열벡터 = 행벡터
열벡터는 OpenGl에서 사용하고 행렬의 오른쪽에 벡터가 있다
행벡터는 Direct 3D에서 사용하고 행렬의 왼쪽에 벡터가 있다.
단위 행렬 (Identity Matrix)
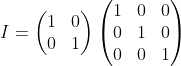
단위 행렬은 어떤 행렬과 곱해도 행렬을 유지함
MI = IM = M
만약 AB = I 이면, 각각의 행렬은 다른 행렬의 역벡터임
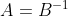
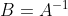
다음의 수식도 성립
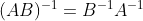
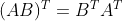
2차원, 3차원 벡터의 좌표계
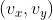
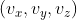
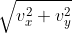
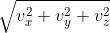
정규화 : 벡터를 벡터의 길이로 나눔
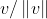
이 것을 단위 벡터로 부르고 길이는 항상 1이다.
좌표계와 기저
좌표계(Coordinate System) = 원점(origin) + 기저(basis)
기저란 모든 벡터를 만들 수 있는 두 개의 벡터 (e1, e2)
Orthonormal Standard Basis : 직교하고 기본이 되는 기저 (0,1) (1,0)
내적 (Dot Product, Inner Product)
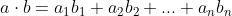
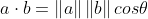
예각일 땐 양수, 둔각일 땐 음수
유닛 벡터 자기 자신과의 내적은 1
위의 특징으로 2D Standard Basis를 보면
자기 자신과의 내적은 1,
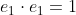
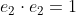
직교하는 벡터와의 내적은 0이다.
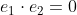
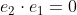
외적 (Cross Product)
3D vector에서만 가능
a × b
외적의 방향 : right-hand rule로 a→b 방향으로 네 손가락을 감을 때 엄지의 방향으로 향한다.
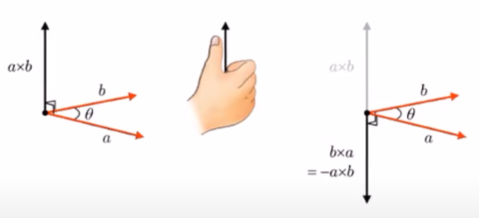
외적의 길이 : a벡터와 b벡터의 평행사변형 넓이
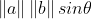
a = b이라면, 외적은 영벡터가 된다.
외적하는 순서가 달라지면 방향만 바뀐다.
계산하는 방법
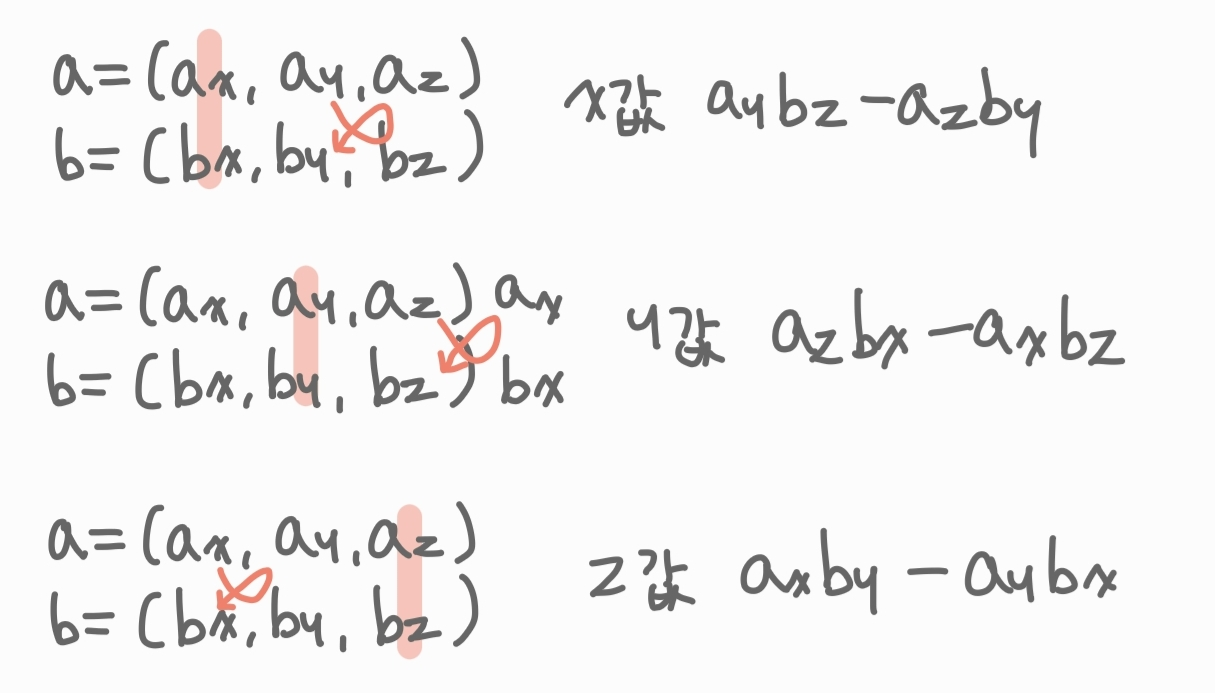
Line과 Ray, 선형 보간
직선을 수식으로 표현하면
점 p0과 p1을 잇는 벡터는 이렇게 표현한다.
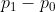
p0와 p1을 잇는 무한한 직선을 수식으로 이렇게 표현할 수 있다.
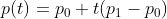
t의 범위가 무한대라면, p(t)는 무한한 직선이고,
t의 범위가 0부터 무한대라면, p(t)는 Ray이다.
t의 범위가 0부터 1이라고 가정
p의 수식을 변형하면 다음과 같다.
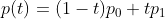
p0이 t=0이 되고, p1이 t=1이 되는데, 선분 내의 모든점은 양 끝점을 보간한다.
p0과 p1을 잇는 선분은 p0과 p1을 선형보간해서 얻을 수 있다.
선분 내 좌표는 다음과 같이 표현한다.
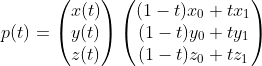
선형 보간의 예 : 양 끝에 색이 있는 선분 내의 색을 채울 때 선형 보간을 통해 얻을 수 있다. (R,G,B)
