'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[2장]
수와 집합
자연수, 정수, 유리수, 실수, 복소수, 사원수
연산과 수의 구조
수집합의 고유한 특징인 원소를 이용한 연산 : 덧셈, 뺄셈, 곱셈, 나눗셈
→ 두 개의 원소를 사용해 새로운 원소를 만들어냄 : 이항연산
이항연산의 성질 : 같은 집합에 속한 두 수를 투입한 이항연산의 결과가 항상 투입한 집합에 속한다면, 그 이항연산은 해당 집합에 대해 닫혀 있다(Closure)고 함
- 교환 법칙 : 순서와 관계 없이 항상 동일한 결과
ex) a+b = b+a, a·b = b∙a - 결합 법칙 : 연산이 두 번 이상 연속될 때, 앞의 연산을 먼저 계산한 결과와 뒤의 연산을 계산한 결과가 같음
ex) (a+b)+c = a+(b+c), (a∙b)∙c = a∙(b∙c) - 분배 법칙 : 서로 다른 2가지 연산에 대해 다음 규칙 성립
a∙(b+c) = a∙b+a∙c, (b+c)∙a = b∙a+c∙a좌분배, 우분배를 모두 만족하면 분배법칙을 만족한다고 함 - 항등원 : 임의의 수와의 연산 결과를 항상 동일한 수로 만들어주는 특별한 수
0은 덧셈의 항등원,1은 곱셈의 항등원 - 역원 : 임의의 수와의 연산 결과를 항상 항등원으로 만들어주는 특별한 수
반대수는 덧셈의 역원,역수는 곱셈의 역원,0의 곱셈 역원은 없다.
수의 구조
어떤 연산에 대해 11가지 공리를 만족하는 수 집합 : 체의 구조
체의 구조를 만족하는 유리수, 실수는 덧셈과 곱셈을 안전하게 사용 가능
뺄셈과 나눗셈은 교환법칙을 만족하지 않아 체의 구조를 지니지 못함
→ 나눗셈 대신 곱셈의 역원, 뺄셈 대신 덧셈의 역원 사용
수의 표현
실수(ℝ)를 이용해 시각화 → 수직선
함수
함수의 개념과 종류
함수의 규칙
- 첫 번째 집합의 모든 원소에 대한 대응 관계 존재
- 첫 번째 집합의 원소는 두 번째 집합의 한 원소에만 대응
정의역 : 함수에서 왼쪽에 위치한 첫 번째 집합
공역 : 함수에서 오른쪽에 위치한 두 번째 집합
치역 : 정의역에 대응되는 공역의 부분 집합
함수의 종류
- 전사함수 : 공역의 모든 요소가 정의역에 대응되는 함수
- 단사함수 : 정의역과 공역의 요소가 일대일로 대응되는 함수
- 전단사함수 : 정의역과 공역의 모든 요소가 빠짐없이 일대일로 대응되는 함수
합성함수
합성 함수 : 2개의 함수를 연쇄적으로 이어 하나의 함수로 만드는 연산
f(x)와 g(y)의 합성함수
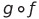
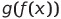
합성 함수는 결합 법칙 성립
항등함수와 역함수
항등 함수 : 정의역과 공역이 동일한 값으로 대응되는 함수
id (항등함수)일 때, id와 f의 합성 함수는 f이다.
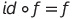
함수와 역함수의 합성 결과는 항등함수
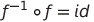
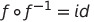
전단사함수의 경우에만 역함수가 보장
합성함수의 역함수
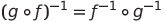
곱집합을 활용한 좌표 평면으로의 확장
집합 A와 B가 있고 각 집합에 속한 원소를 a, b라고 했을 때 집합 A와 B의 곱집합
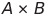
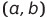
실수 집합 ℝ을 확장해 두 실수 집합의 곱집합 ℝ×ℝ은 평면으로 나타낼 수 있음
'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[2장]
수와 집합
자연수, 정수, 유리수, 실수, 복소수, 사원수
연산과 수의 구조
수집합의 고유한 특징인 원소를 이용한 연산 : 덧셈, 뺄셈, 곱셈, 나눗셈
→ 두 개의 원소를 사용해 새로운 원소를 만들어냄 : 이항연산
이항연산의 성질 : 같은 집합에 속한 두 수를 투입한 이항연산의 결과가 항상 투입한 집합에 속한다면, 그 이항연산은 해당 집합에 대해 닫혀 있다(Closure)고 함
- 교환 법칙 : 순서와 관계 없이 항상 동일한 결과
ex) a+b = b+a, a·b = b∙a - 결합 법칙 : 연산이 두 번 이상 연속될 때, 앞의 연산을 먼저 계산한 결과와 뒤의 연산을 계산한 결과가 같음
ex) (a+b)+c = a+(b+c), (a∙b)∙c = a∙(b∙c) - 분배 법칙 : 서로 다른 2가지 연산에 대해 다음 규칙 성립
a∙(b+c) = a∙b+a∙c, (b+c)∙a = b∙a+c∙a좌분배, 우분배를 모두 만족하면 분배법칙을 만족한다고 함 - 항등원 : 임의의 수와의 연산 결과를 항상 동일한 수로 만들어주는 특별한 수
0은 덧셈의 항등원,1은 곱셈의 항등원 - 역원 : 임의의 수와의 연산 결과를 항상 항등원으로 만들어주는 특별한 수
반대수는 덧셈의 역원,역수는 곱셈의 역원,0의 곱셈 역원은 없다.
수의 구조
어떤 연산에 대해 11가지 공리를 만족하는 수 집합 : 체의 구조
체의 구조를 만족하는 유리수, 실수는 덧셈과 곱셈을 안전하게 사용 가능
뺄셈과 나눗셈은 교환법칙을 만족하지 않아 체의 구조를 지니지 못함
→ 나눗셈 대신 곱셈의 역원, 뺄셈 대신 덧셈의 역원 사용
수의 표현
실수(ℝ)를 이용해 시각화 → 수직선
함수
함수의 개념과 종류
함수의 규칙
- 첫 번째 집합의 모든 원소에 대한 대응 관계 존재
- 첫 번째 집합의 원소는 두 번째 집합의 한 원소에만 대응
정의역 : 함수에서 왼쪽에 위치한 첫 번째 집합
공역 : 함수에서 오른쪽에 위치한 두 번째 집합
치역 : 정의역에 대응되는 공역의 부분 집합
함수의 종류
- 전사함수 : 공역의 모든 요소가 정의역에 대응되는 함수
- 단사함수 : 정의역과 공역의 요소가 일대일로 대응되는 함수
- 전단사함수 : 정의역과 공역의 모든 요소가 빠짐없이 일대일로 대응되는 함수
합성함수
합성 함수 : 2개의 함수를 연쇄적으로 이어 하나의 함수로 만드는 연산
f(x)와 g(y)의 합성함수
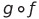
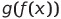
합성 함수는 결합 법칙 성립
항등함수와 역함수
항등 함수 : 정의역과 공역이 동일한 값으로 대응되는 함수
id (항등함수)일 때, id와 f의 합성 함수는 f이다.
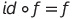
함수와 역함수의 합성 결과는 항등함수
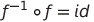
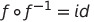
전단사함수의 경우에만 역함수가 보장
합성함수의 역함수
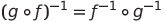
곱집합을 활용한 좌표 평면으로의 확장
집합 A와 B가 있고 각 집합에 속한 원소를 a, b라고 했을 때 집합 A와 B의 곱집합
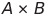
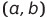
실수 집합 ℝ을 확장해 두 실수 집합의 곱집합 ℝ×ℝ은 평면으로 나타낼 수 있음
