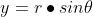'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[4장]
삼각함수
삼각비 : 직각삼각형을 구성하는 세 변에서 두 변을 뽑아 각각의 비례관계를 나타낸 것
사인, 코사인, 탄젠트
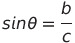
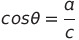
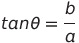
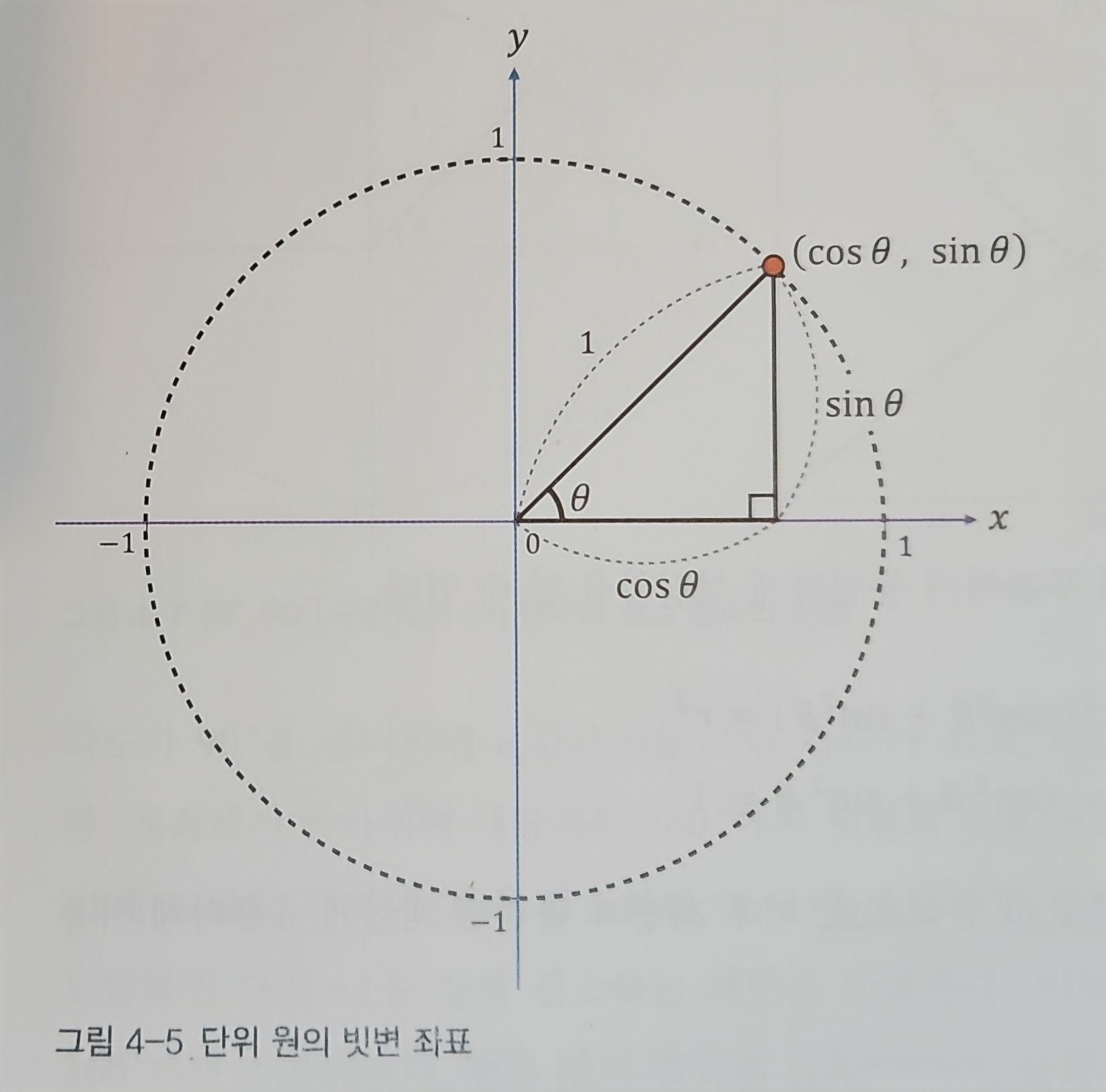
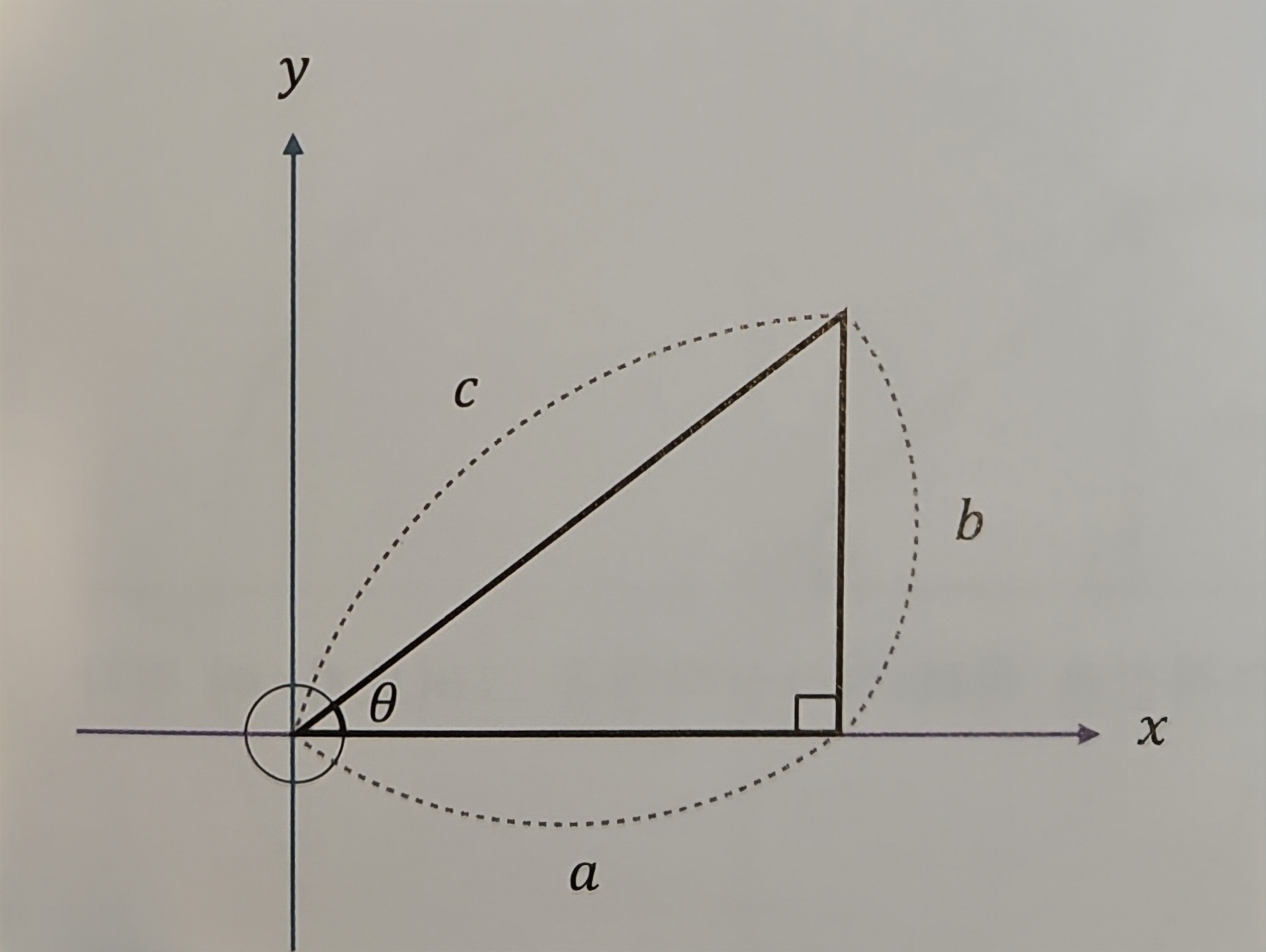
단위 원 위의 좌표는
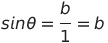
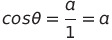
피타고라스 정리에 의해 해당 공식을 얻을 수 있음
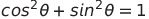
단위 원의 반지름을 r로 일반화
→ 길이가 1인 벡터와 평행, 길이는 r배 증가
→ 스칼라 곱셈에 의해 r⋅(cosθ, sinθ)
→ 밑변의 길이 r⋅cosθ, 높이의 길이 r⋅sinθ
삼각함수의 성질
데카르트 좌표계의 각도 : x축에서 원의 궤적을 따라 반시계 방향으로 회전한 크기
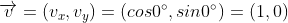
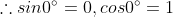
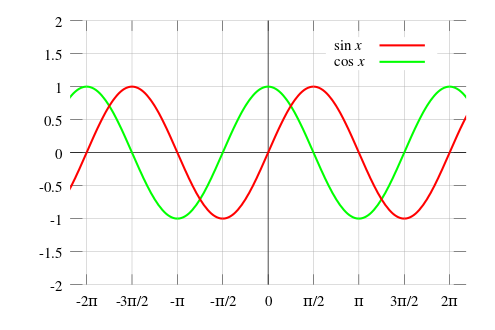
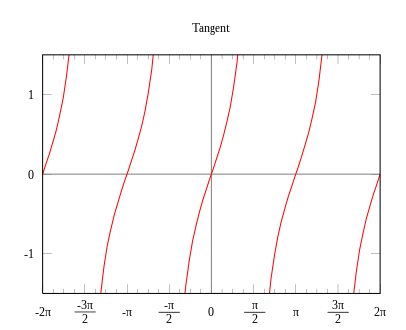
- sin 함수와 cos 함수는 항상 -1에서 1 사이를 일정하게 반복하는 패턴을 띤다.
- sin 함수와 cos 함수의 값은 360° 주기로 반복된다.
- y축을 기준으로 좌우를 접어 포갰을 때 cos 함수 그래프는 좌우 대칭(짝함수, 우함수), sin 함수 그래프는 원점 대칭(홀함수, 기함수)
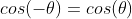
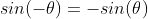
tan 함수는 빗변과 무관하게 밑변과 높이의 관계만을 나타냄
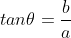
모두 빗변 값으로 나누면
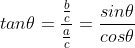
분모의 값은 0이 될 수 없기 때문에 분모에 해당하는 cos 함수 값이 0이 되는 90°에서는 tan 값이 존재하지 않음
tan 함수는 홀함수의 성질
각의 측정법
각도법 : 0에서 360까지의 수 사용
호도법 : 호의 길이를 기준으로 각을 측정, 호의 길이가 1이 되는 부채꼴의 각을 기준으로 각을 측정
반원(180도)의 호의 길이는 파이
호의 길이가 1인 각 : 1rad(라디안)
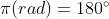
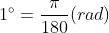
삼각함수를 활용한 물체의 회전
회전은 x와 y값이 함께 영향을 미치기 때문에, x축과 y축을 분리해 독립적으로 계산할 수 없음
여기서 사용하는 것이 기저벡터
회전을 위해 실벡터 공간 ℝ² 전체를 θ만큼 회전하면
e₁과 e₂의 좌표는 다음과 같이 변화됨
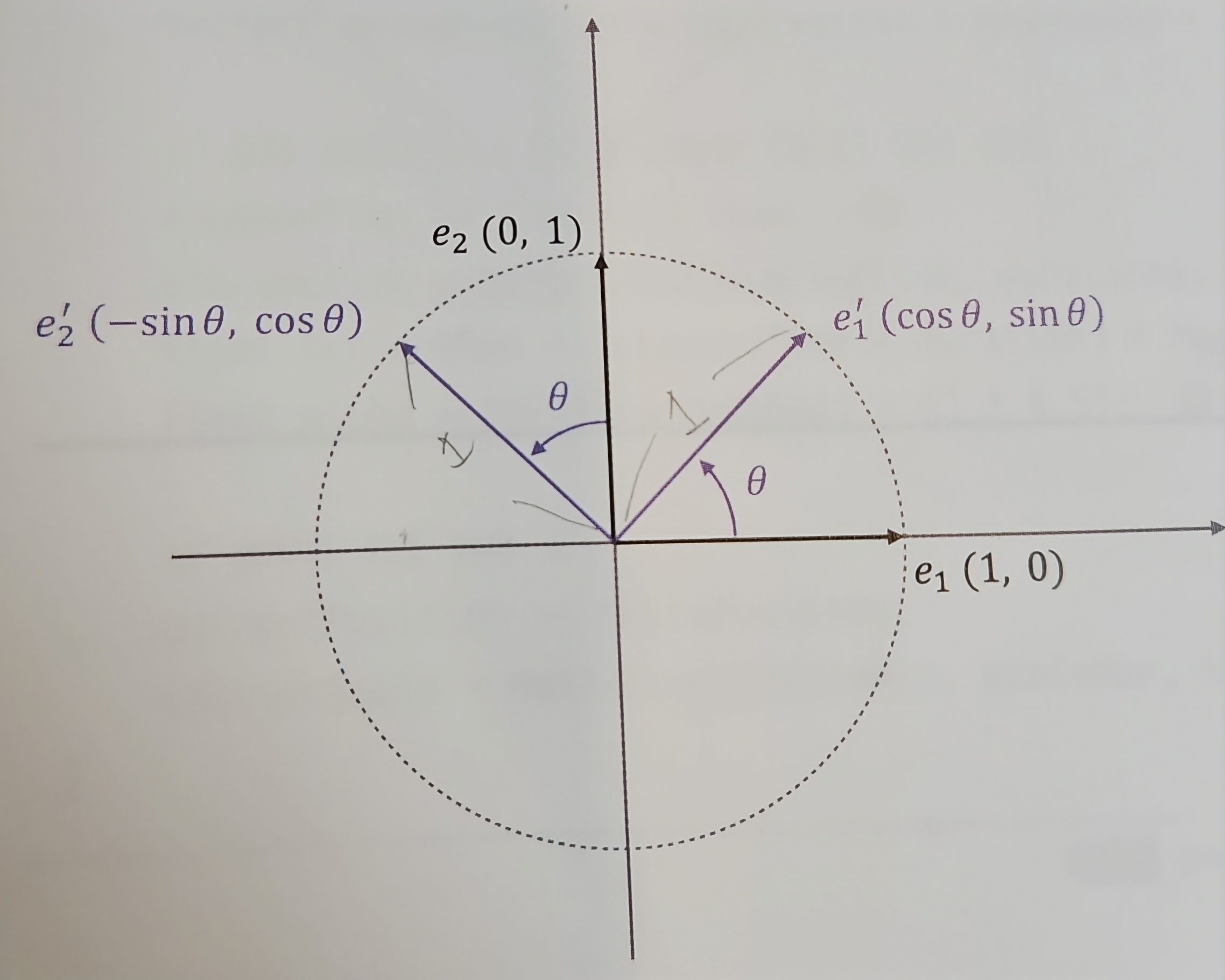
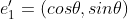
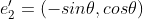
회전되기 전 벡터를 표준기저벡터를 사용해 선형 결합식으로 표현하면
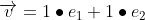
회전 후 벡터에 회전된 표준기저벡터를 치환하면
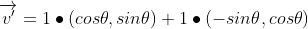
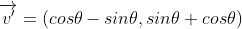
임의의 벡터 (x,y)가 θ만큼 회전
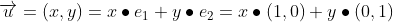
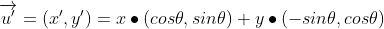
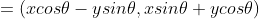
회전의 결과는
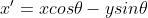
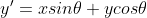
삼각함수의 역함수
좌표로부터 각도를 구할 때 사용
arcsin(아크사인) 함수 : 정의역([-90°, 90°])과 공역([-1,1])의 범위를 제한시켜 얻은 sin 함수의 역함수
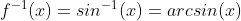
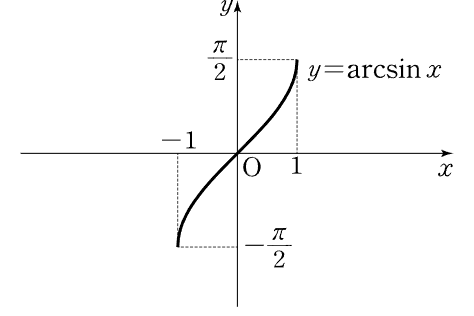
arccos(아크코사인) 함수 : 정의역([0°, 180°])과 공역([-1,1])의 범위를 제한시켜 얻은 cos 함수의 역함수
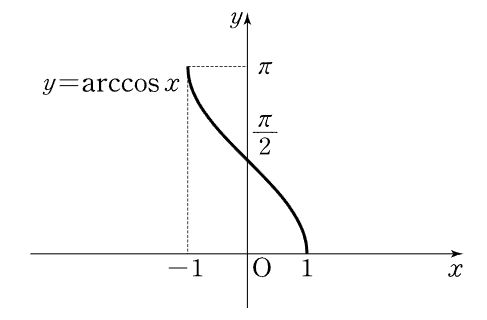
arctan(아크탄젠트) 함수 : 정의역(-90°, 90°를 제외한 (-90°, 90°))의 범위를 제한시켜 얻은 tan 함수의 역함수
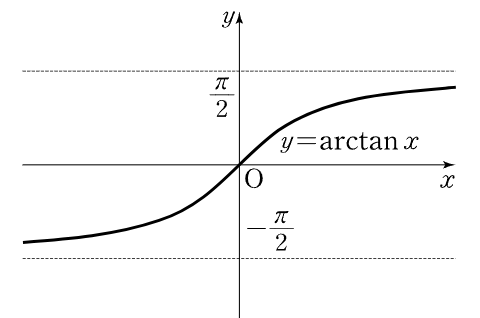
arctan 함수는 벡터의 각도를 구하는 데 유용함
임의의 벡터를 분수식으로 계산해 벡터로부터 tan 함수 값을 얻고, 이 값을 arctan 함수에 넣으면 해당 벡터가 x축과 이루는 사잇각을 얻을 수 있음
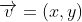
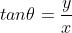
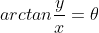
삼각함수의 역함수로 얻을 수 있는 각의 범위는 한계되어 있음
→ arctan의 경우, 인자에 분수값을 넣지 않고 x,y 두 값을 분리해 전달하면 4사분면 전체에 해당하는 각의 정보를 얻을 수 있음
ex) 제 3사분면과 같이 x도 음수, y도 음수인 벡터의 사잇각 구하기
→ 원래는 y/x가 양수 값이라 1사분면 각의 정보만 나옴
→ x와 y 값을 따로 전달하면 두 값이 가지는 부호를 파악해 벡터가 1사분면에 있었는지, 3사분면에 있었는지 파악 가능
그래서 arctan 함수에는 분수값(y/x)를 계산해 전달하는 함수, x와 y를 따로 전달하는 함수 두 종류가 있음
극좌표계
데카르트 좌표계 회전 : x와 y의 변화를 매번 계산해야 함
극좌표계 : 원점으로부터의 거리 r과 각 θ의 두 요소로 구성, 극좌표계의 좌표 (r, θ)로 표시
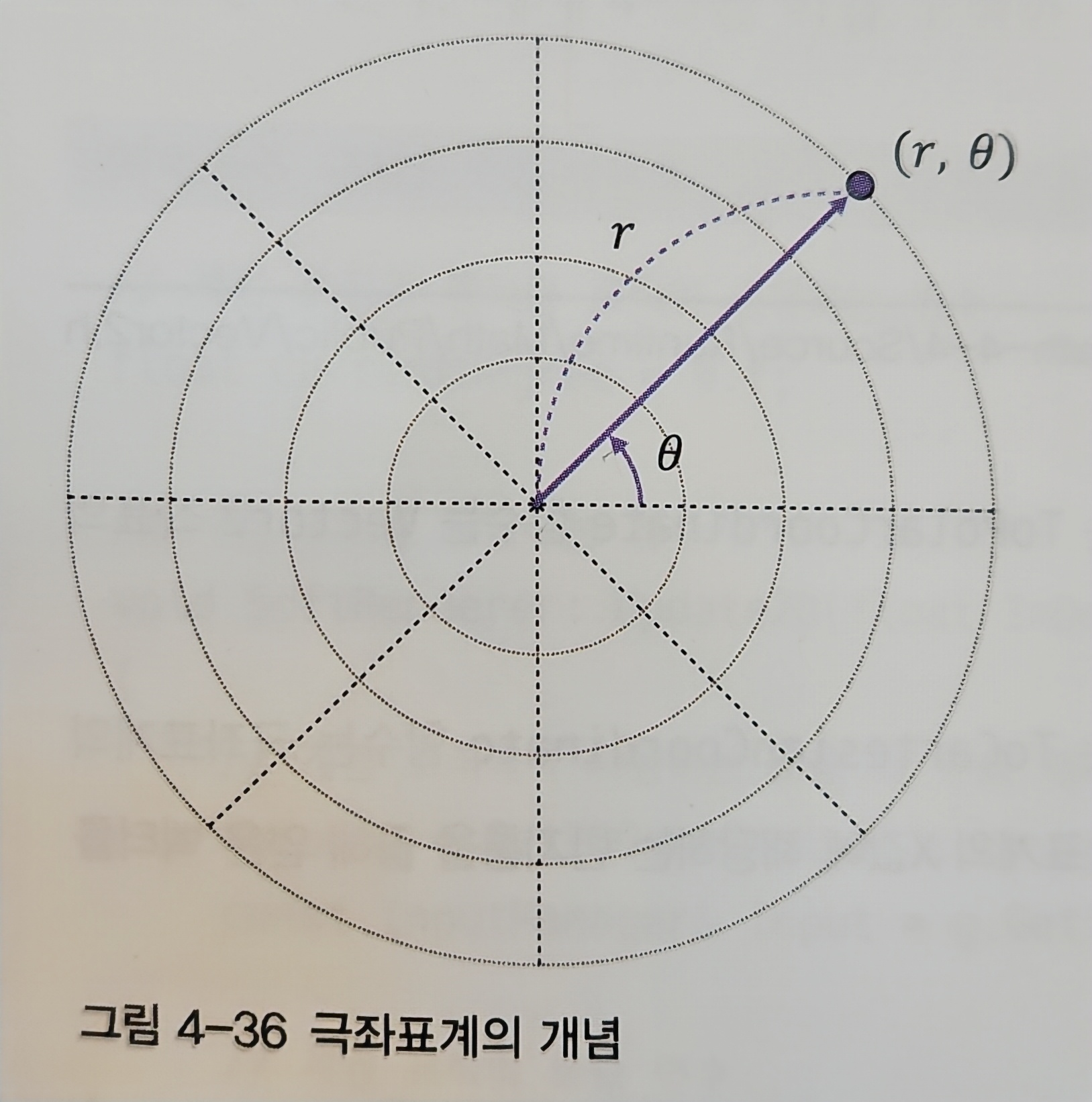
데카르트 좌표계로 표현된 벡터 (x,y) → 극좌표계 (r,θ)
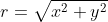
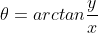
극좌표계 (r,θ) → 데카르트 좌표계 (x,y)