[KUOCW] 한정현 컴퓨터그래픽스를 듣고 정리한 포스팅입니다.
모델링 (Modeling)
렌더링 할 물체 생성
폴리곤 메시 (Polygon Mesh)
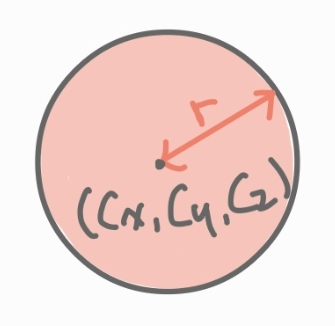
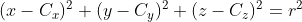
구를 정의하면 위와 같은 음함수로 만들어짐
→ GPU에선 음함수를 처리하기에 적합 X
표면의 점 → 샘플 → 일정한 개수 꼭짓점(정점)으로 만듦
폴리곤 (Polygon)
삼각형 메시를 일반적으로 사용
꼭짓점 개수 × 2 = 삼각형 개수 (대강)
맥스나 마야같은 모델링 프로그램에선 사각형 메시를 사용하는데,
이를 두 개의 삼각형으로 나눔
해상도, LOD (Resolution, Level of Detail)
정점의 개수(해상도)를 얼마정도로 할지 정해야 함
어느 정도 해상도로 할지?
: 물체가 화면 상에 얼마만한 크기로 나오는지에 따라 다름
ex) 물체가 작게 나온다면 해상도를 높일 필요가 없고, 물체가 크게 나온다면 해상도를 높여야 할 것
폴리곤 메시의 컴퓨터에서의 표현
폴리곤 메시가 주어질 때 어떻게 표현이 되는지
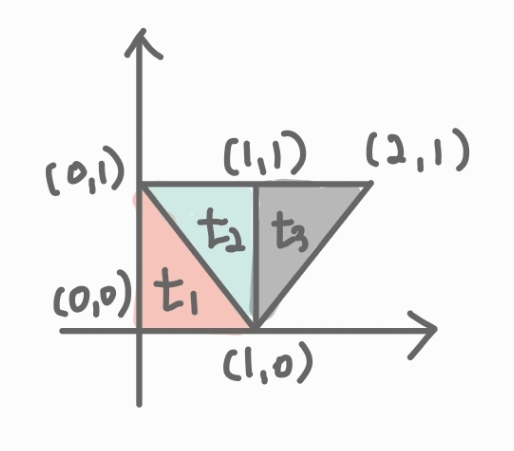
Vertex Array
| vertex array | |
| (0,0) | t1 |
| (1,0) | |
| (0,1) | |
| (1,0) | t2 |
| (1,1) | |
| (0,1) | |
| (1,1) | t3 |
| (1,0) | |
| (2,1) | |
삼각형 정점들에 대한 vertex array 구성
→ 중복되는 점이 많다는 문제점
Vertex Array와 Index Array
| vertex array | |
| 0 | (0,0) |
| 1 | (0,1) |
| 2 | (1,0) |
| 3 | (1,1) |
| 4 | (2,1) |
| index array | |
| 0 | t1 |
| 2 | |
| 1 | |
| 2 | t2 |
| 3 | |
| 1 | |
| 3 | t3 |
| 2 | |
| 4 | |
중복되지 않게 정점들에 대한 vertex array를 만들고,
vertex array의 인덱스를 가져와 삼각형 메시의 정점에 대한 index array를 만듦
→ index array는 2B, 4B와 같이 크기가 같지만 vertex array는 각 정점의 위치 정보 이외의 다른 정보가 많아 크기가 큼
⇒ 해당 방식이 일반적
법선 벡터 (Surface Normals)
vertex array의 다른 정보 중 하나
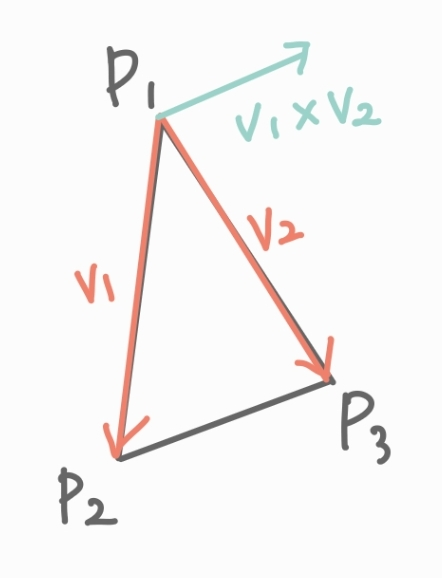
(P1, P2, P3) 삼각형 메시에 대한 법선 벡터 구하기
: v1, v2 벡터에 대해 오른손 법칙 적용
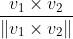
법선 벡터는 단위 벡터로 표현하기 때문에 외적을 길이로 나누어줌
세 꼭짓점의 시계 반대 방향으로 (CCW)
→ 삼각형 메시가 (P1, P3, P2)일 때는 물체의 안쪽 방향으로 법선 벡터가 향함
→ 컴퓨터 그래픽스에선 모든 법석이 물체 바깥으로 되야 함
⇒ 반시계 방향으로 정점 나열
정점 Normal
폴리곤 메시밖에 없을 때 정점 법선 벡터 계산
→ 정점을 공유하는 삼각형 메시 법선 벡터의 평균
Export and Import
| application1 (Max ..) |
→ (export) |
file (.obj) |
→ (import) |
application2 (Unity ..) |
Obj 파일의 구성
ex) 26개의 정점, 48개의 삼각형 메시가 있는 구를 export 했을 때
v (vertex) (x,y,z) ... 26개의 정점
vn (vertex normal) (x,y,z) ... 26개의 정점 법선(정점 노말 값이 같은건 하나만 저장)
f (face) (정점, 정점, 정점) ... 48개의 면 (정점 : v//vn으로 구성)
각 정점에 대한 vertex array : 정점의 개수만큼
| vertex array | |
| position | normal |
| 26개의 vertex array | |
삼각형 메시에 대한 index array
: vertex array에 대한 인덱스로 구성 : 삼각형 메쉬 개수 × 3
| index array |
| 0 |
| 1 |
| 2 |
| ... |
| 144개의 index array (48×3) |
