[게임 수학] 내적: 벡터 공간의 분석과 응용

'이득우의 게임 수학' 책을 보고 정리한 글입니다.

[7장]

---

벡터의 내적 (Dot product)

같은 차원의 벡터 두개를 스칼라로 만들어내는 연산

$$ \vec{u} = (a,b) $$

$$ \vec{v} = (c,d) $$

$$ \vec{u}\cdot\vec{v} = a\cdot c + b\cdot d $$

 

내적의 성질

• 교환 법칙 : 스칼라의 곱셈과 덧셈으로 구성되어 있어서

$$ \vec{u}\cdot\vec{v} = \vec{v} \cdot \vec{u} $$

• 결합 법칙 X : 벡터가 아닌 스칼라로 나와서

$$ \vec{u}\cdot(\vec{v}\cdot\vec{w}) \neq (\vec{u}\cdot\vec{v})\cdot\vec{w} $$

• 덧셈에 대한 분배 법칙

$$ \vec{w}\cdot(\vec{u}+\vec{v}) = \vec{u}\cdot\vec{w} + \vec{v}\cdot\vec{w} $$

• 같은 벡터를 내적하면 벡터의 크기를 제곱한 결과

$$ (x,y) \cdot (x,y) = x^2 + y^2 $$

$$ \vec{v}\cdot\vec{v} = |\vec{v}|^2 $$

→ 벡터 크기의 정의 : 자신을 내적한 결과의 제곱근

 

두 벡터 합의 내적은 두 벡터의 크기로 표현

$$ (\vec{u}+\vec{v})\cdot(\vec{u}+\vec{v}) = \vec{u}\cdot\vec{u}+\vec{v}\cdot\vec{v} +2(\vec{u}\cdot\vec{v}) $$

$$ = |\vec{u}|^2 + |\vec{v}|^2 + 2(\vec{u}\cdot \vec{v}) $$

 

내적과 삼각함수와의 관계

\(cos\) 함수와 비례

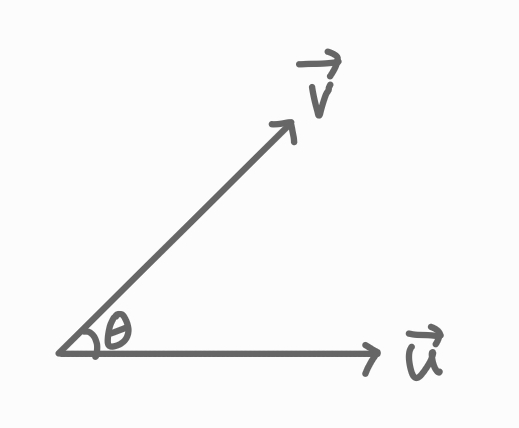
$$ \vec{u}\cdot\vec{v} = |\vec{u}||\vec{v}|cos\theta $$

 

두 벡터의 크기가 1이면, 두 벡터의 내적은 \(cos\) 함수

$$ \vec{u}\cdot\vec{v} = cos\theta $$

 

두 벡터의 내적의 값이 0이면, 두 벡터는 직교함

→ 벡터 공간에서 직교하는 두 표준기저벡터 (1,0)과 (0,1)을 내적한 결과는 항상 0

 

행렬의 곱셈을 내적으로 표현하기

행렬과 벡터의 곱셈 연산

$$ \begin{bmatrix}a & b \\c & d \\\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} =\begin{bmatrix}ax+by\\cx+dy\end{bmatrix}  $$

→ 두 개의 행벡터 \( (a,b),(c,d) \)와 벡터를 구성하는 열벡터 \( (x,y) \) 내적으로 표현 가능

$$ \begin{bmatrix}ax+by \\ cx+dy\end{bmatrix} = \begin{bmatrix}(a,b)\cdot(x,y) \\ (c,d)\cdot(x,y)\end{bmatrix} $$

 

행렬의 곱셈 → 벡터의 내적으로 표현 가능

$$ \begin{bmatrix}a & b \\c & d \\\end{bmatrix} \begin{bmatrix}e & f \\g & h \\\end{bmatrix} = \begin{bmatrix}ae+bg & af+bh \\ce+dg & cf+dh \\\end{bmatrix} = \begin{bmatrix}(a,b)\cdot(e,g) & (a,b)\cdot(f,h) \\ (c,d)\cdot(e,g) & (c,d)\cdot(f,h) \\\end{bmatrix} $$

 

직교 행렬

• 정방행렬을 구성하는 모든 행벡터와 열벡터의 크기가 1
• 벡터들이 서로 직교

 

직교 행렬 \(Q\)

• \( (a,b), (b,d), (a,c), (c,d) \)의 크기 1
• \((a,b), (c,d)\)는 서로 직교

$$ Q = \begin{bmatrix}a & c \\b & d \\\end{bmatrix} $$

 

직교행렬의 전치행렬은 역행렬

$$ Q\cdot Q^T = I $$

 

회전 변환행렬은 각 행벡터와 열벡터의 크기가 1이고, 서로 직교

→ 직교행렬

$$ R_\theta = \begin{bmatrix}cos\theta & -sin\theta \\sin\theta & cos\theta \\\end{bmatrix} $$

 

선형 변환 중 물체의 형태가 그대로 유지되는 선형 변환

→ 강체 변환

 

선형 변환이 강체 변환이 되기 위한 조건

1. 변화된 기저벡터의 크기는 모두 1
2. 모든 기저벡터는 서로 직교
3. 행렬식 값이 1

 

회전 변환은 1,2번의 조건은 만족, 행렬식 \(ad - bc\)의 값은 1이 됨 → 강체 변환

$$ det(R) = cos^2\theta + sin^2\theta = 1 $$

 

시야 판별

앞뒤 판별

목표물이 캐릭터의 앞에 있는지, 뒤에 있는지 구분 → 내적의 부호

 

\(cos\)함수는 -90º에서 90º까지(분홍색 부분) 양의 부호

 

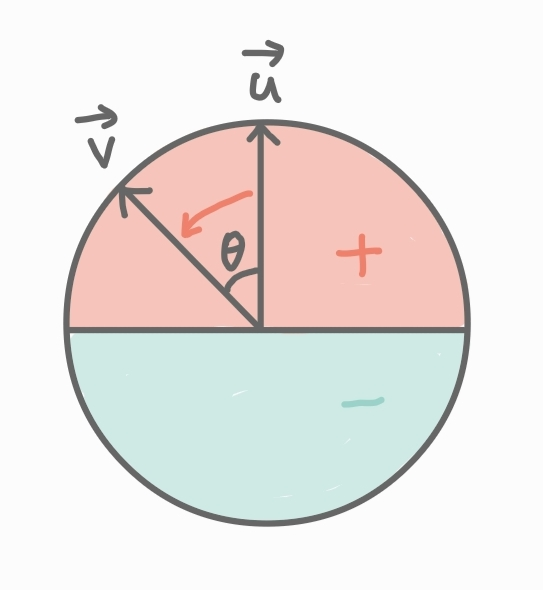
내적의 부호만 가지고 두 벡터의 방향 파악 가능

• 벡터 내적의 결과가 양수 : 두 벡터는 같은 방향을 향함
• 벡터 내적의 결과가 음수 : 두 벡터는 다른 방향을 향하고 있음, 서로 마주보고 있음(벡터는 위치의 개념X)
• 벡터 내적의 결과가 0 : 두 벡터는 서로 직교함

 

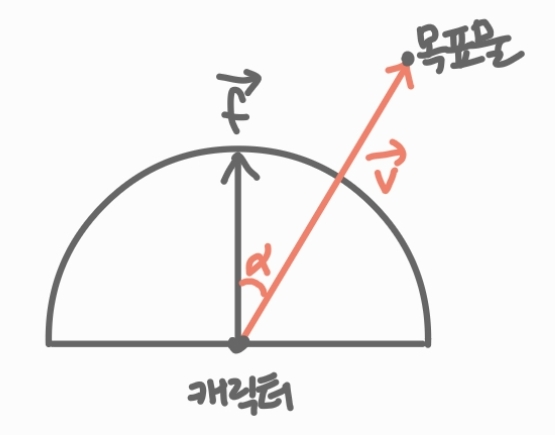
캐릭터가 바라보는 방향 \(\vec{f}\)

캐릭터에서 목표물로 향하는 벡터 \(\vec{v}\)

그 사이의 각 \(\alpha\)

• \(\vec{f}\cdot\vec{v}\) 결과의 부호가 양수 : 캐릭터 앞에 목표물이 있음
• \(\vec{f}\cdot\vec{v}\) 결과의 부호가 음수 : 캐릭터 뒤에 목표물이 있음
• \(\vec{f}\cdot\vec{v}\) 결과의 부호가 0 : 캐릭터 옆에 목표물이 있음

 

시야 판별

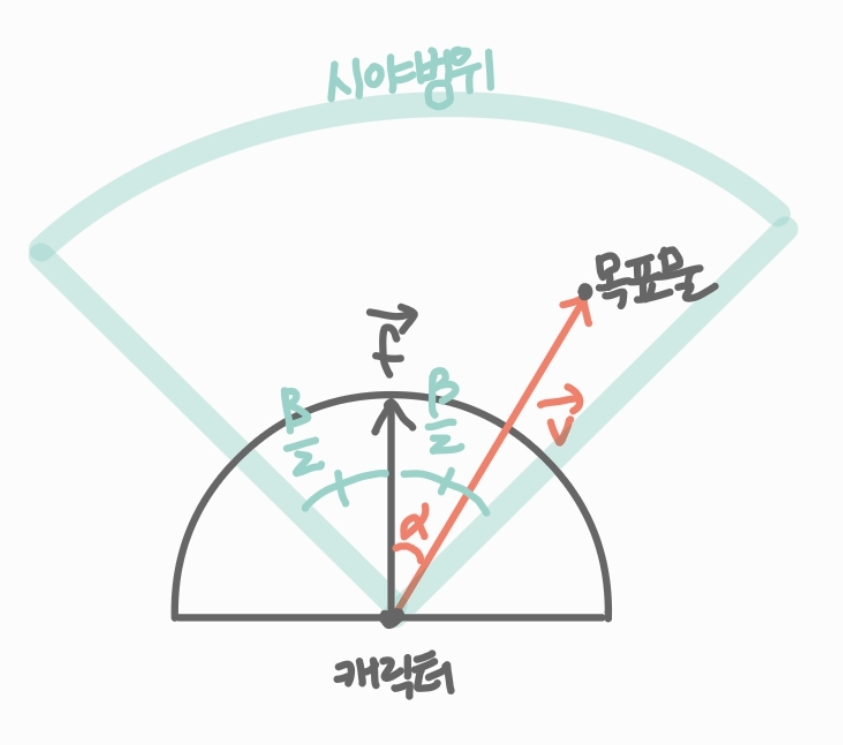
캐릭터에 부여한 시야각 \(\beta\)

캐릭터가 바라보는 방향 \(\vec{f}\)

캐릭터에서 목표물로 향하는 벡터 \(\vec{v}\)

그 사이의 각 \(\alpha\)

 

→ 사잇각 \(\alpha\)가 시야각의 절반인 \(\frac{\beta}{2}\)보다 작거나 같은지 비교

 

\(cos\) 함수는 [0º, 180º] 범위에서 각이 커질수록 값이 작아짐

→ 이를 이용해 내적의 값의 결과인 \(cos\alpha\)와 \(cos\frac{\beta}{2}\) 값을 비교

 

1. 시야각의 절반 나눈 각의 \(cos\frac{\beta}{2}\)를 미리 계산
2. 캐릭터의 시선 벡터를 구해 이의 크기를 1로 정규화 → 단위 벡터 \(\hat{f}\)
3. 캐릭터에서 목표물로 향하는 벡터도 1로 정규화 → 단위 벡터 \(\hat{v}\)
4. 내적 \(\hat{f}\cdot\hat{v}\)의 계산 결과는 \(cos\alpha\). 이를 \(cos\frac{\beta}{2}\)와 비교

 

\(cos\)함수의 성질을 이용해 다음과 같이 판단

• \(\hat{f}\cdot\hat{v} \geq cos\frac{\beta}{2}\) : 목표물이 시야 범위 안에 있음
• \(\hat{f}\cdot\hat{v} \leq cos\frac{\beta}{2}\) : 목표물이 시야 범위 밖에 있음

 

조명 효과의 구현

램버트 반사 모델 : 현실 세계와 비슷한 조명 효과, 컴퓨터 그래픽스에서 표면에서의 조명 모델 계산을 위해 쓰임

 

빛을 받아 표면에서 반사되는 빛의 세기는 두 벡터가 만드는 사잇각의 \(cos\) 함수에 비례

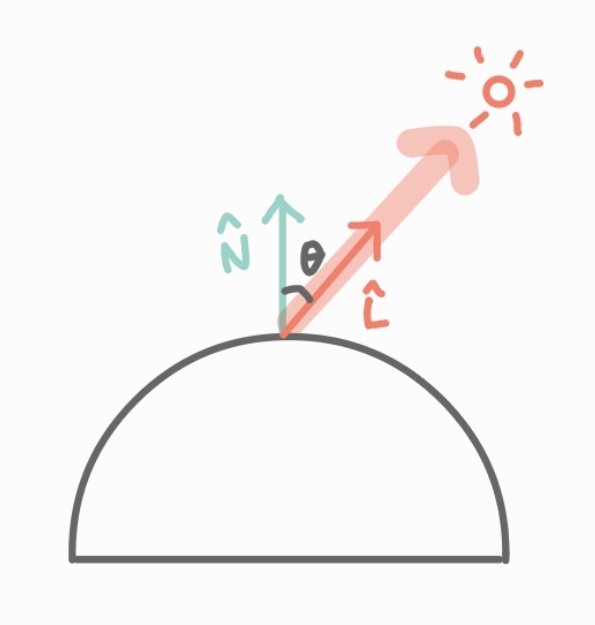
표면이 향하는 단위 벡터 \(\hat{N}\)

표면에서 광원으로 향하는 단위 벡터 \(\hat{L}\)

→ 두 벡터의 내적을 사용해 램버트 반사 모델에 필요한 사잇각의 \(cos\)값을 얻을 수 있음

\[ \hat{N}\cdot \hat{L} = cos\theta \]

 

투영 벡터

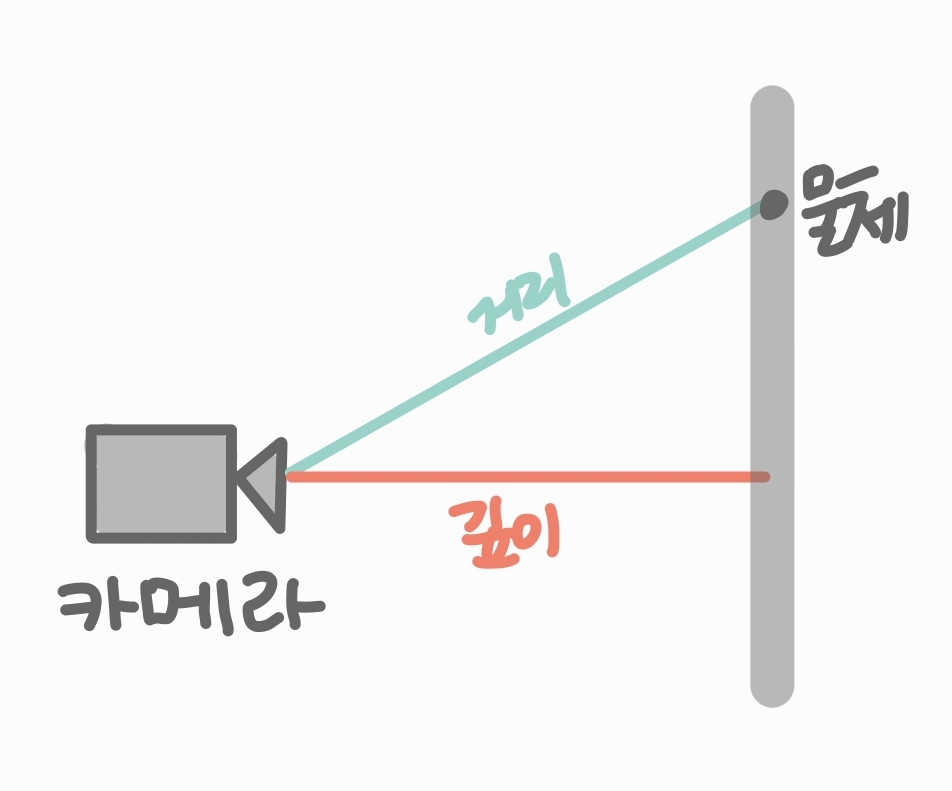
벡터 내적은 어떤 벡터를 다른 벡터에 직교 투영하는 용도로 사용

ex) 카메라에서 물체까지의 깊이 값

 

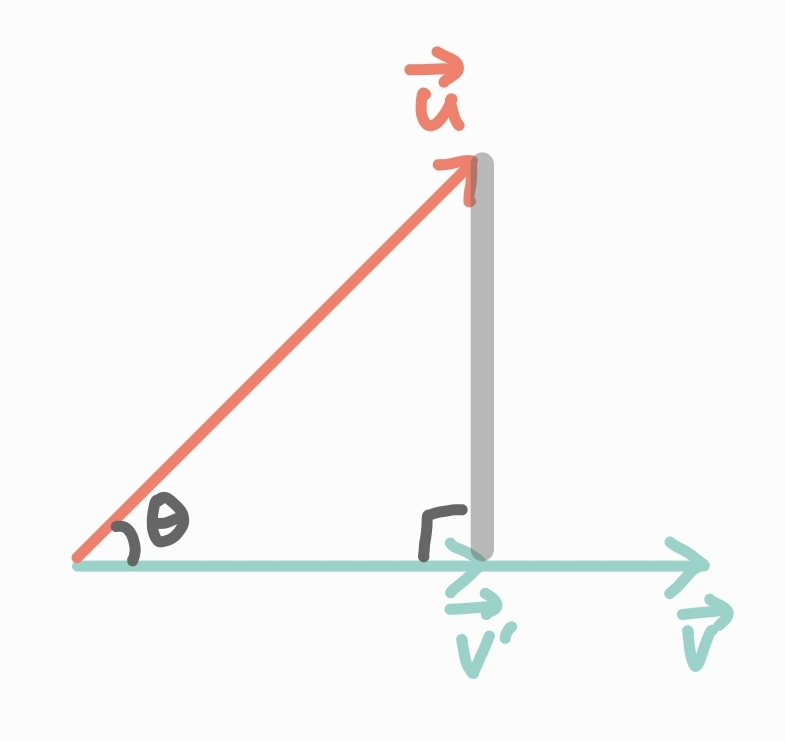
벡터 \(\vec{u}\)를 벡터 \(\vec{v}\)에 투영

→ 투영 벡터 \(\vec{v'}\)

 

\(\vec{v}\)를 정규화시킨 단위벡터 \(\hat{v}\)에 \(\vec{v'}\)의 크기를 곱하면 투영 벡터를 구할 수 있음

$$ \vec{v'} = |\vec{v'}|\cdot \hat{v} $$

 

해당 수식을 전개하면

$$ \vec{v'} = |\vec{v'}|\cdot \hat{v} $$

$$ = |\vec{v'}|\cdot \frac{\vec{v}}{|\vec{v}|} $$

$$ = |\vec{u}|\cdot cos\theta \cdot \frac{\vec{v}}{|\vec{v}|} $$

$$ = |\vec{u}|\cdot \frac{\vec{u}\cdot\vec{v}}{|\vec{u}||\vec{v}|} \cdot \frac{\vec{v}}{|\vec{v}|} $$

$$ = \frac{(\vec{u}\cdot\vec{v})}{|\vec{v}|^2} \cdot \vec{v} $$

$$ = \frac{(\vec{u}\cdot\vec{v})}{(\vec{v}\cdot\vec{v})} \cdot \vec{v} $$

 

투영할 벡터 \(\vec{v}\)의 크기가 1이면 단순하게 정리됨

$$ \vec{v'} = (\vec{u}\cdot\vec{v})\cdot\vec{v} $$