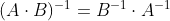'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[5장]
선형성: 예측 가능한 비례 관계
원점에서 시작하는 벡터와 스칼라 곱셈으로 생성된 벡터는 원점을 지나는 직선 상에 위치함
선형성 : 직선의 형태를 띠는 성질
수학에서의 선형성 : 두 가지 조건을 모두 만족하는 함수의 성질
- 가법성
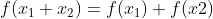
- 1차 동차성
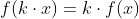
선형 함수
원점을 지나는 직선의 함수
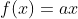
위의 조건에 만족하는지 알기 위해 x 대신 해당 값들을 넣어 좌변과 우변 값을 비교한다.
성립하므로 선형성을 만족한다.
하지만, f(x) = ax + b 와 같은 원점을 지나지 않는 함수는 가법성을 만족하지 못해 선형성을 만족하지 못함
선형성 : 두 집합의 순수한 비로 구성된 1차적 대응 관계
벡터 공간의 선형 변환
2차원 벡터를 입출력으로 사용하는 선형성을 가지는 함수
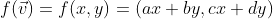
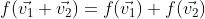
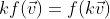
가법성과 1차 동차성에 대해 만족하기 때문에 선형 함수
표준기저벡터의 선형 결합으로 형성된 벡터 공간 → 선형성을 지님
이 벡터 공간을 선형 함수로 변화시킨 새로운 공간도 기저벡터의 선형 결합으로 형성 → 선형성을 지님
=> 두 공간이 동일한 구조를 지닐 때 두 공간의 대응 관계를 변환(Transformation)이라고 부름
=> 선형성을 유지시켜주는 선형함수는 선형 변환(Linear Transformation)이라고 함
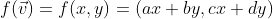
벡터 공간에서 발생하는 선형 변환의 원리는 크기 변환, 회전 변환과 관련
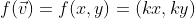
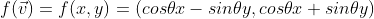
=> 각각 a,b,c,d에 알맞은 값을 대입하면 선형 변환임을 알 수 있음
벡터 공간에서의 선형 변환
→ 두 집합의 순수한 비를 통해 예측할 수 있는 형태로 변환
→ 역함수를 통해 변환 후의 벡터로부터 변환 전의 벡터를 파악 가능
행렬
n개의 행과 m개의 열로 이루어진 사각형의 형태
선형 변환과 벡터를 나타낼 때 사용
- 벡터 : 한 줄로, A는 열벡터, B는 행벡터
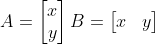
- 선형 변환 : 행과 열이 같은 정방행렬(Square Matrix), f(x,y) = (ax + by, cx + dy)를 2 × 2 정방행렬로 표현할 때 대응하는 A
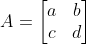
정방 행렬 A는 2개의 열벡터 또는 2개의 행벡터로 구성
행벡터 : (a,b) (c,d)
열벡터 : (a,c) (b,d)
행렬의 기본 연산
행렬과 행렬의 덧셈
행렬의 크기가 같은 경우에만
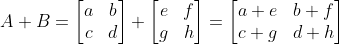
행렬과 스칼라의 곱셈
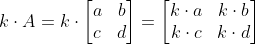
행렬의 전치 (Transpose of a matrix)
전치연산은 첨자 T로 표시, 행과 열을 바꾸는 작업
대각 성분의 원소는 그대로 유지, 나머지 원소는 대각 성분을 중심으로 대칭된 행렬

행렬과 행렬의 곱셈
행렬의 곱셈은 앞에 위치한 행렬의 행벡터와 뒤에 위치한 행렬의 열벡터를 각각 곱하고 더함
- 교환 법칙 성립 X
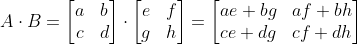
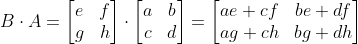
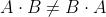
- 결합 법칙 만족
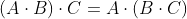
- 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해 곱한 결과와 같음
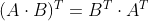
a,b,c,d 네 개의 원소로 구성된 2×2 정방행렬과 2차원 벡터 (x,y)를 열벡터로 설정한 두 행렬의 곱은
2차원 벡터 공간의 선형 변환 f(x,y) = (ax+by, cx+dy)와 같음
2×2 정방행렬은 2차원 공간의 선형 변환에 대응되는 함수
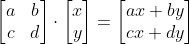
→ 2차원 벡터에 선형 변환을 적용해 새로운 벡터를 생성하는 작업
벡터에 선형 변환을 적용하기 위한 연산 순서는 오른쪽에서 왼쪽 방향으로
정방행렬의 곱셈
2×2 정방행렬이 2차원 벡터 공간의 선형 변환에 대응되니 → 2×2 정방행렬 간의 곱은 합성 함수에 대응되는 연산
벡터 v에 선형 변환을 나타내는 2×2 정방행렬 A, B를 순서대로 연산한다면
왼쪽에서 오른쪽으로 진행되므로
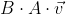
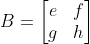
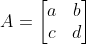
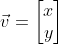
라고 했을 때, 벡터 v가 선형 변환을 통해 w가 되는 과정은 다음과 같다.

합성함수는 결합법칙을 만족하기 때문에 다음과 같다
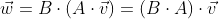
결합법칙이 성립하는 행렬의 곱은 컴퓨터 그래픽 연산에 유용하게 활용됨
물체의 점을 각각 v1~v100까지 있고, 선형 변환을 수행하는 행렬 A,B,C,D,E가 있다고 하면
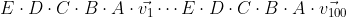
각 5번씩 100번 연산해서 500번 해야할 텐데,
결합법칙으로 A,B,C,D,E 연산을 미리 구해두고 각각의 점에 곱해주면 104번의 연산만 하면된다.
(참고) 열 기준 행렬과 행 기준 행렬
보통은 벡터를 열벡터로 나타내는 열 기준 행렬을 사용하는데,
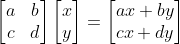
이렇게 행 기준 행렬을 사용할 때는 벡터가 행렬 앞에 있어야 하고, 행렬은 전치시켜야 한다.
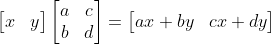
행 기준 방식으로는 DirectX, 언리얼 엔진 C++
열 기준 방식으로는 OpenGL, 유니티 엔진 C#
행렬 곱셈에 대한 전치연산의 성질 때문에 위와 같이 바뀐다.
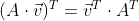
열 기준 행렬은 오른쪽에서 왼쪽 방향으로 진행되지만
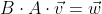
행 기준 행렬은 열 기준 행렬의 전치이므로 다음과 같이 바뀐다.
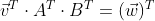
행렬의 설계
평면상의 물체를 우리가 원하는 형태로 변환하기 위해 2×2 행렬을 설계하는 방법
벡터 공간 V를 구성하는 두 표준기저벡터 (1,0) (0,1)이 선형변환을 통해 → (a,c) (b,d)로 변환
벡터 공간 V의 벡터 v는 표준기저벡터의 선형 결합을 통해 생성
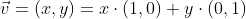
벡터 v가 선형 변환되는 경우에도
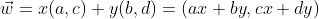
→ 이는 a,b,c,d로 만들어진 정방행렬에 벡터 (x,y)를 곱한 결과와 같음
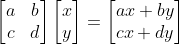
두 벡터 (a,c) (b,d)는 정방행렬을 구성하는 열벡터
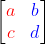
크기 변환행렬
물체의 크기를 변경하는 행렬
표준기저 벡터 (1,0) e1을 a배 늘리거나 줄인 벡터
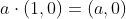
표준기저 벡터 (0,1) e2를 b배 늘리거나 줄인 벡터
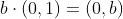
변환된 표준기저 벡터를 열벡터로 설정해 생성한 크기 변환행렬
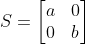
회전 변환행렬
각 θ로 벡터 공간을 회전시키는 회전 변환행렬
반시계 방향 90º 회전한 (1,0) 표준 기저벡터 → (0,1)
반시계 방향 90º 회전한 (0,1) 표준 기저벡터 → (-1,0)
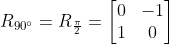
시계 방향 90º 회전한 (1,0) 표준 기저벡터 → (0,-1)
시계 방향 90º 회전한 (0,1) 표준 기저벡터 → (1,0)
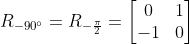
θ만큼 회전한 (1,0) 표준 기저벡터 → (cosθ, sinθ)
θ만큼 회전한 (0,1) 표준 기저벡터 → (-sinθ, cosθ)
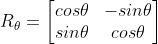
전단 변환행렬
표준기저벡터 e1을 고정한 상태에서 표준기저벡터 e2를 x축 방향으로 미는 변환
대각으로 밀리는 형태
x축 방향으로 1만큼 미는 전단 변환
표준기저 벡터 e1의 변환 결과 : (1,0)로 변화없음
표준기저 벡터 e2의 변환 결과 : (1,1)
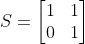
x축 방향으로 a만큼 미는 전단 변환
표준기저 벡터 e1의 변환 결과 : (1,0)로 변화없음
표준기저 벡터 e2의 변환 결과 : (a,1)
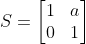
삼각함수의 덧셈 정리
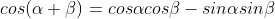
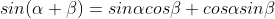
회전 변환에 사용하는 두 각 α와 β가 있을 때
α+β의 회전한 변환 = 두 각에 대한 회전 변환을 순서대로 적용한 결과
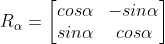
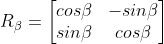
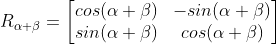
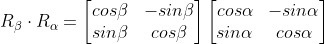
덧셈 정리를 응용해서 배각 공식도 만들 수 있음
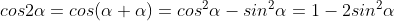
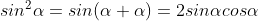
역행렬
항등행렬 : 원 공간의 변화 X, 동일한 공간 유지
I로 표시
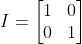
역행렬 : 행렬 곱의 결과가 항등행렬이 나오는 행렬
벡터 공간 V가 선형 변환된 벡터 공간 W에서 V로 되돌리는 선형 변환
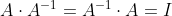
역행렬의 존재를 판별하는 행렬식
행렬식 : 어떤 행렬의 역행렬이 존재하는지 판별, det()으로 표시
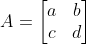
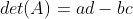
det(A) = 0인 선형 변환 : 전단사 대응이 성립하지 않아 역행렬이 존재하지 않음
두 기저벡터의 기울기가 같으면 차원이 줄어들어 (평면 → 직선) 거꾸로 변환되는 것이 불가능해짐
행렬식의 원리 : 두 벡터가 이루는 평행사변형의 넓이
→ 행렬식의 값이 0이 되면 평행사변형의 넓이 소멸되어 2차원으로 돌아갈 수 없음
행렬식 계산 결과가 음수 : 평면이 뒤집힘
크기 변환행렬의 역행렬
원 공간에서 x축을 a배, y축을 b배 크기 변화시킨 크기 변환행렬 S
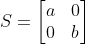
S의 역행렬 : a, b의 역수를 대입
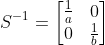
전단 변환행렬의 역행렬
표준기저벡터 e1을 고정한 상태로 e2를 a만큼 민 전단 변환행렬 S
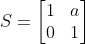
S의 역행렬 : a의 반대수 대입
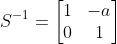
회전 변환행렬의 역행렬
θ만큼 회전한 회전 변환행렬 R
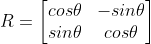
R의 역행렬 : -θ를 대입
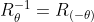
sin과 cos의 다음과 같은 성질을 이용해 정리
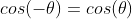
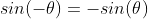
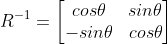
이는 R의 전치행렬과 같음
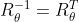
행렬 곱의 역행렬
합성함수의 역함수와 동일하게 수식 성립
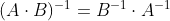
'이득우의 게임 수학' 책을 보고 정리한 글입니다.
[5장]
선형성: 예측 가능한 비례 관계
원점에서 시작하는 벡터와 스칼라 곱셈으로 생성된 벡터는 원점을 지나는 직선 상에 위치함
선형성 : 직선의 형태를 띠는 성질
수학에서의 선형성 : 두 가지 조건을 모두 만족하는 함수의 성질
- 가법성
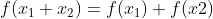
- 1차 동차성
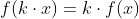
선형 함수
원점을 지나는 직선의 함수
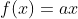
위의 조건에 만족하는지 알기 위해 x 대신 해당 값들을 넣어 좌변과 우변 값을 비교한다.
성립하므로 선형성을 만족한다.
하지만, f(x) = ax + b 와 같은 원점을 지나지 않는 함수는 가법성을 만족하지 못해 선형성을 만족하지 못함
선형성 : 두 집합의 순수한 비로 구성된 1차적 대응 관계
벡터 공간의 선형 변환
2차원 벡터를 입출력으로 사용하는 선형성을 가지는 함수
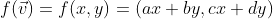
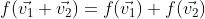
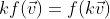
가법성과 1차 동차성에 대해 만족하기 때문에 선형 함수
표준기저벡터의 선형 결합으로 형성된 벡터 공간 → 선형성을 지님
이 벡터 공간을 선형 함수로 변화시킨 새로운 공간도 기저벡터의 선형 결합으로 형성 → 선형성을 지님
=> 두 공간이 동일한 구조를 지닐 때 두 공간의 대응 관계를 변환(Transformation)이라고 부름
=> 선형성을 유지시켜주는 선형함수는 선형 변환(Linear Transformation)이라고 함
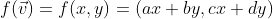
벡터 공간에서 발생하는 선형 변환의 원리는 크기 변환, 회전 변환과 관련
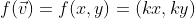
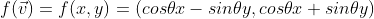
=> 각각 a,b,c,d에 알맞은 값을 대입하면 선형 변환임을 알 수 있음
벡터 공간에서의 선형 변환
→ 두 집합의 순수한 비를 통해 예측할 수 있는 형태로 변환
→ 역함수를 통해 변환 후의 벡터로부터 변환 전의 벡터를 파악 가능
행렬
n개의 행과 m개의 열로 이루어진 사각형의 형태
선형 변환과 벡터를 나타낼 때 사용
- 벡터 : 한 줄로, A는 열벡터, B는 행벡터
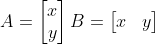
- 선형 변환 : 행과 열이 같은 정방행렬(Square Matrix), f(x,y) = (ax + by, cx + dy)를 2 × 2 정방행렬로 표현할 때 대응하는 A
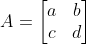
정방 행렬 A는 2개의 열벡터 또는 2개의 행벡터로 구성
행벡터 : (a,b) (c,d)
열벡터 : (a,c) (b,d)
행렬의 기본 연산
행렬과 행렬의 덧셈
행렬의 크기가 같은 경우에만
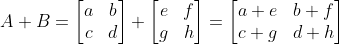
행렬과 스칼라의 곱셈
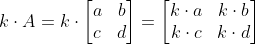
행렬의 전치 (Transpose of a matrix)
전치연산은 첨자 T로 표시, 행과 열을 바꾸는 작업
대각 성분의 원소는 그대로 유지, 나머지 원소는 대각 성분을 중심으로 대칭된 행렬

행렬과 행렬의 곱셈
행렬의 곱셈은 앞에 위치한 행렬의 행벡터와 뒤에 위치한 행렬의 열벡터를 각각 곱하고 더함
- 교환 법칙 성립 X
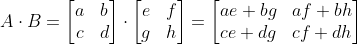
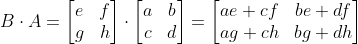
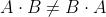
- 결합 법칙 만족
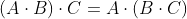
- 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해 곱한 결과와 같음
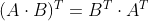
a,b,c,d 네 개의 원소로 구성된 2×2 정방행렬과 2차원 벡터 (x,y)를 열벡터로 설정한 두 행렬의 곱은
2차원 벡터 공간의 선형 변환 f(x,y) = (ax+by, cx+dy)와 같음
2×2 정방행렬은 2차원 공간의 선형 변환에 대응되는 함수
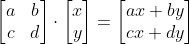
→ 2차원 벡터에 선형 변환을 적용해 새로운 벡터를 생성하는 작업
벡터에 선형 변환을 적용하기 위한 연산 순서는 오른쪽에서 왼쪽 방향으로
정방행렬의 곱셈
2×2 정방행렬이 2차원 벡터 공간의 선형 변환에 대응되니 → 2×2 정방행렬 간의 곱은 합성 함수에 대응되는 연산
벡터 v에 선형 변환을 나타내는 2×2 정방행렬 A, B를 순서대로 연산한다면
왼쪽에서 오른쪽으로 진행되므로
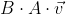
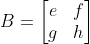
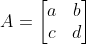
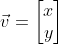
라고 했을 때, 벡터 v가 선형 변환을 통해 w가 되는 과정은 다음과 같다.

합성함수는 결합법칙을 만족하기 때문에 다음과 같다
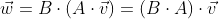
결합법칙이 성립하는 행렬의 곱은 컴퓨터 그래픽 연산에 유용하게 활용됨
물체의 점을 각각 v1~v100까지 있고, 선형 변환을 수행하는 행렬 A,B,C,D,E가 있다고 하면
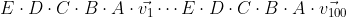
각 5번씩 100번 연산해서 500번 해야할 텐데,
결합법칙으로 A,B,C,D,E 연산을 미리 구해두고 각각의 점에 곱해주면 104번의 연산만 하면된다.
(참고) 열 기준 행렬과 행 기준 행렬
보통은 벡터를 열벡터로 나타내는 열 기준 행렬을 사용하는데,
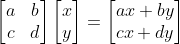
이렇게 행 기준 행렬을 사용할 때는 벡터가 행렬 앞에 있어야 하고, 행렬은 전치시켜야 한다.
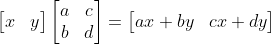
행 기준 방식으로는 DirectX, 언리얼 엔진 C++
열 기준 방식으로는 OpenGL, 유니티 엔진 C#
행렬 곱셈에 대한 전치연산의 성질 때문에 위와 같이 바뀐다.
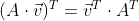
열 기준 행렬은 오른쪽에서 왼쪽 방향으로 진행되지만
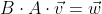
행 기준 행렬은 열 기준 행렬의 전치이므로 다음과 같이 바뀐다.
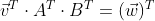
행렬의 설계
평면상의 물체를 우리가 원하는 형태로 변환하기 위해 2×2 행렬을 설계하는 방법
벡터 공간 V를 구성하는 두 표준기저벡터 (1,0) (0,1)이 선형변환을 통해 → (a,c) (b,d)로 변환
벡터 공간 V의 벡터 v는 표준기저벡터의 선형 결합을 통해 생성
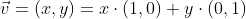
벡터 v가 선형 변환되는 경우에도
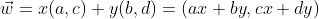
→ 이는 a,b,c,d로 만들어진 정방행렬에 벡터 (x,y)를 곱한 결과와 같음
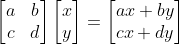
두 벡터 (a,c) (b,d)는 정방행렬을 구성하는 열벡터

크기 변환행렬
물체의 크기를 변경하는 행렬
표준기저 벡터 (1,0) e1을 a배 늘리거나 줄인 벡터
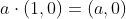
표준기저 벡터 (0,1) e2를 b배 늘리거나 줄인 벡터
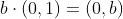
변환된 표준기저 벡터를 열벡터로 설정해 생성한 크기 변환행렬
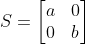
회전 변환행렬
각 θ로 벡터 공간을 회전시키는 회전 변환행렬
반시계 방향 90º 회전한 (1,0) 표준 기저벡터 → (0,1)
반시계 방향 90º 회전한 (0,1) 표준 기저벡터 → (-1,0)
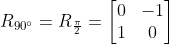
시계 방향 90º 회전한 (1,0) 표준 기저벡터 → (0,-1)
시계 방향 90º 회전한 (0,1) 표준 기저벡터 → (1,0)
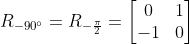
θ만큼 회전한 (1,0) 표준 기저벡터 → (cosθ, sinθ)
θ만큼 회전한 (0,1) 표준 기저벡터 → (-sinθ, cosθ)
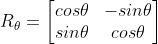
전단 변환행렬
표준기저벡터 e1을 고정한 상태에서 표준기저벡터 e2를 x축 방향으로 미는 변환
대각으로 밀리는 형태
x축 방향으로 1만큼 미는 전단 변환
표준기저 벡터 e1의 변환 결과 : (1,0)로 변화없음
표준기저 벡터 e2의 변환 결과 : (1,1)
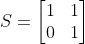
x축 방향으로 a만큼 미는 전단 변환
표준기저 벡터 e1의 변환 결과 : (1,0)로 변화없음
표준기저 벡터 e2의 변환 결과 : (a,1)
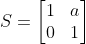
삼각함수의 덧셈 정리
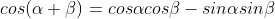
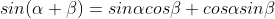
회전 변환에 사용하는 두 각 α와 β가 있을 때
α+β의 회전한 변환 = 두 각에 대한 회전 변환을 순서대로 적용한 결과
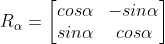
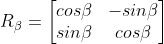
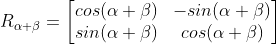
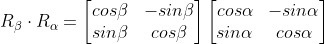
덧셈 정리를 응용해서 배각 공식도 만들 수 있음
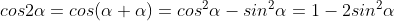
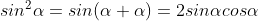
역행렬
항등행렬 : 원 공간의 변화 X, 동일한 공간 유지
I로 표시
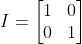
역행렬 : 행렬 곱의 결과가 항등행렬이 나오는 행렬
벡터 공간 V가 선형 변환된 벡터 공간 W에서 V로 되돌리는 선형 변환
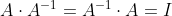
역행렬의 존재를 판별하는 행렬식
행렬식 : 어떤 행렬의 역행렬이 존재하는지 판별, det()으로 표시
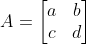
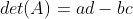
det(A) = 0인 선형 변환 : 전단사 대응이 성립하지 않아 역행렬이 존재하지 않음
두 기저벡터의 기울기가 같으면 차원이 줄어들어 (평면 → 직선) 거꾸로 변환되는 것이 불가능해짐
행렬식의 원리 : 두 벡터가 이루는 평행사변형의 넓이
→ 행렬식의 값이 0이 되면 평행사변형의 넓이 소멸되어 2차원으로 돌아갈 수 없음
행렬식 계산 결과가 음수 : 평면이 뒤집힘
크기 변환행렬의 역행렬
원 공간에서 x축을 a배, y축을 b배 크기 변화시킨 크기 변환행렬 S
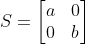
S의 역행렬 : a, b의 역수를 대입
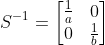
전단 변환행렬의 역행렬
표준기저벡터 e1을 고정한 상태로 e2를 a만큼 민 전단 변환행렬 S
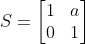
S의 역행렬 : a의 반대수 대입
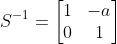
회전 변환행렬의 역행렬
θ만큼 회전한 회전 변환행렬 R
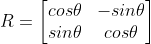
R의 역행렬 : -θ를 대입
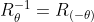
sin과 cos의 다음과 같은 성질을 이용해 정리
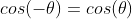
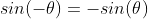
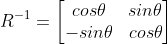
이는 R의 전치행렬과 같음
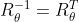
행렬 곱의 역행렬
합성함수의 역함수와 동일하게 수식 성립